Ist die Winkelsumme in einem Dreieck wirklich immer gleich? Schauen wir uns an, was wir machen können. Wir zeichnen ein beliebiges Dreieck:
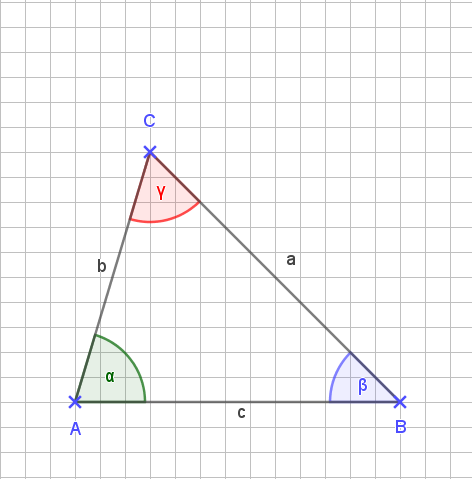
Wir verlängern anschließend alle Seiten des Dreiecks nach beiden Seiten. Dann zeichnen wir eine Parallele zu c durch den Punkt C des Dreiecks.
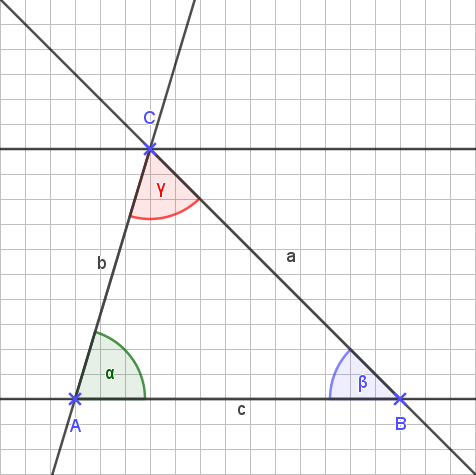
Jetzt müssen wir nur noch die Grundsätze aus dem KapitelWinkelbeziehungen hernehmen und das Dreieck damit untersuchen:
Betrachten wir die Winkel α und α‘.
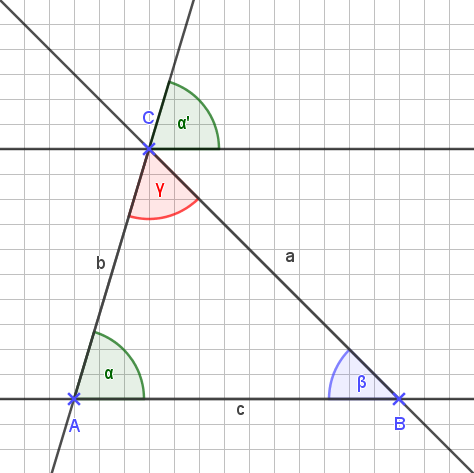
Das sind Stufenwinkel und daher sind beide gleich groß.
α = α‘
Schauen wir uns β und β‘ an.
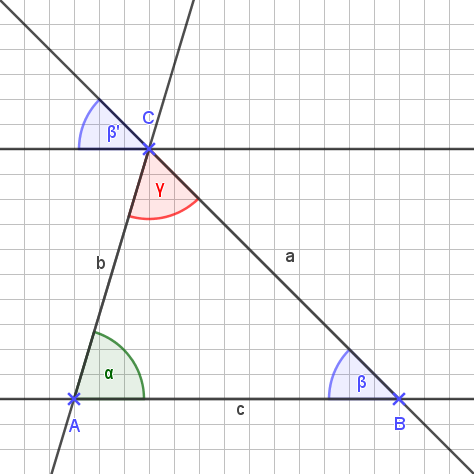
Auch das sind Stufenwinkel und es gilt:
β = β‘
Bleibt noch γ: Auch hier gibt es einen zugehörigen Winkel γ‘.
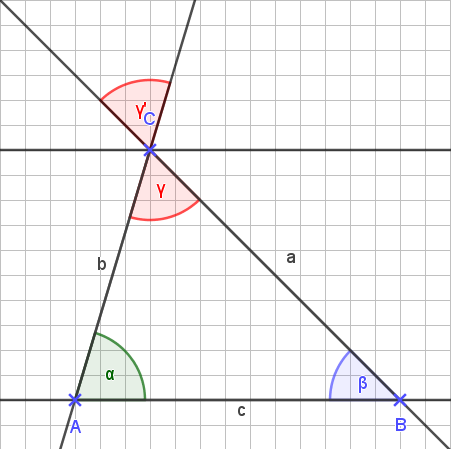
γ und γ‘ sind gegenüberliegende Scheitelwinkel und daher gilt:
γ = γ‘
Betrachten wir nun α‘, β‘ und γ‘ zusammen, so sehen wir:
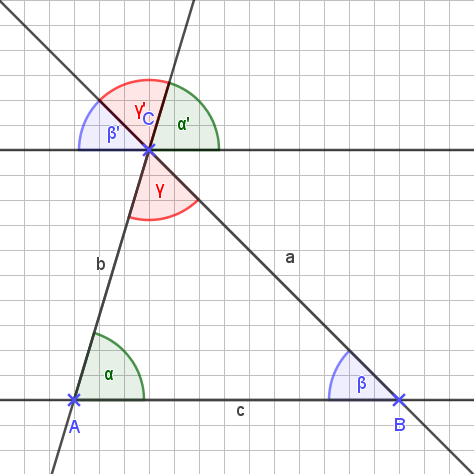
α‘ + β‘ + γ‘ = 180°
Damit gilt auch
α + β + γ = 180°
Somit haben wir bewiesen:
Die Winkelsumme im Dreieck beträgt immer 180°