Wenn wir in der Mathematik mit Winkeln arbeiten, gibt es ein paar einfache Gesetzmäßigkeiten, die uns das Arbeiten mit Winkeln und der Berechnung von fehlenden Winkeln sehr hilfreich sind. Im Folgenden habe ich die wichtigsten Gesetzmäßigkeiten zusammengestellt:
Nebenwinkel?Wenn ich an einer Geraden im Punkt S einen Winkel α abtrage, so erhalte ich gleichzeitig noch einen zweiten Winkel β.
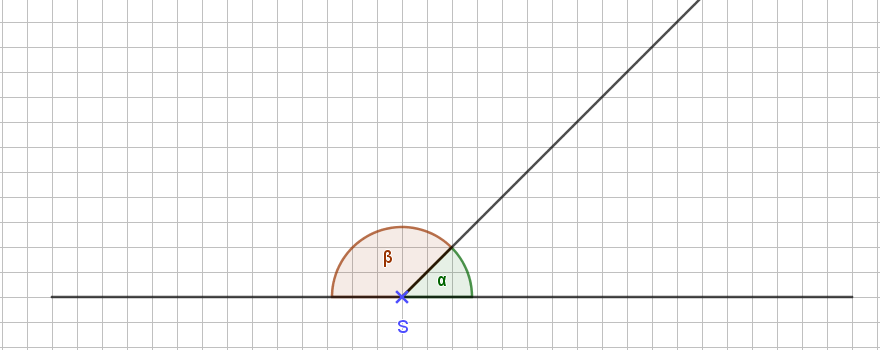
Den Winkel β nennen wir den Nebenwinkel zum Winkel α. Wir sehen sofort:
α + β = 180°
Oder in Worten:
Ein Winkel und sein Nebenwinkel ergänzen sich immer zu 180°.
Das war doch gar nicht so schwer. Gehen wir weiter und lassen sich zwei Geraden kreuzen.
Wenn zwei Geraden sich kreuzen, erhalten wir im Schnittpunkt vier Winkel. Der Schnittpunkt ist der Scheitelpunkt aller vier Winkel, weswegen wir sie Scheitelwinkel nennen. Schauen wir uns das an:
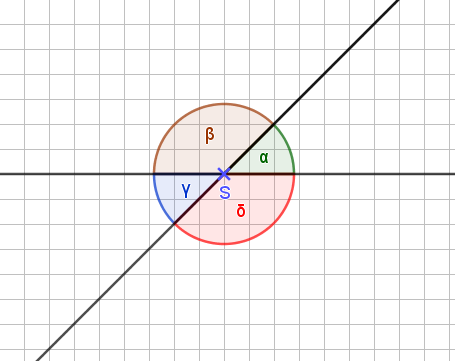
Wir sehen sofort, dass sich alle vier Winkel zu einem Kreis ergänzen, also zusammen 360° groß sind. Als Formel:
α + β + γ + δ = 360°
Schauen wir nach weiteren Beziehungen. Wir wissen bereits: β ist Nebenwinkel zu α. Daher gilt:
α + β = 180°
Es ist aber auch δ Nebenwinkel zu γ. Also gilt:
γ + δ = 180°
Bislang ist das nicht so schwer 😉. Bleibt das auch so? Aber klar! Es gibt nämlich noch weitere Beziehungen, die leicht zu erfassen sind. Schauen wir uns die Winkel α und γ an. Die sind nämlich gleich groß. Dasselbe gilt für die Winkel β und δ. Daraus folgt ganz einfach zu merken:
Gegenüberliegende Scheitelwinkel sind gleich groß.
Wir können also statt γ auch schreiben α‘ und statt δ schreiben wir β‘.
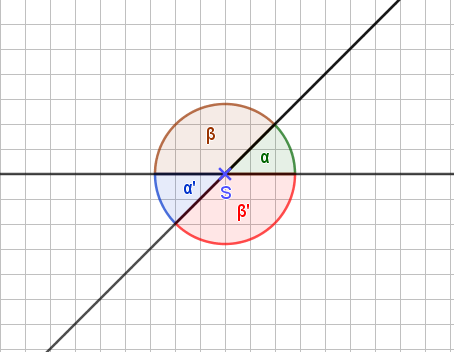
Bringt uns das etwas? Aber klar! Ich brauche bei solchen Konstrukten nämlich nur einen Winkel zu kennen und kann die anderen drei gleich ausrechnen.
Ein Beispiel:
Nehmen wir an, α = 45°. Dann wissen wir sofort: α‘ = 45° (gegenüberliegende Scheitelwinkel). Weil gilt (Winkel und Nebenwinkel):
α + β = 180°
wissen wir auch: β = 135°. Damit gilt auch: β‘ = 135°. Überprüfen wir, ob wir richtig gerechnet haben. Wir wissen ja, der Wert aller vier Winkel addiert sich zu 360°:
α + β + α‘ + β‘ = 360°
45° + 135° + 45° + 135° = 360°
Super, alles stimmt 😊.
Was machen wir aber, wenn sich nicht zwei Geraden in einem Punkt schneiden, sondern 3, 4, 5…. Okay, nehmen wir uns drei Geraden vor. Das gesagte gilt dann auch entsprechend für 4, 5… Geraden, die sich in einem Punkt schneiden.
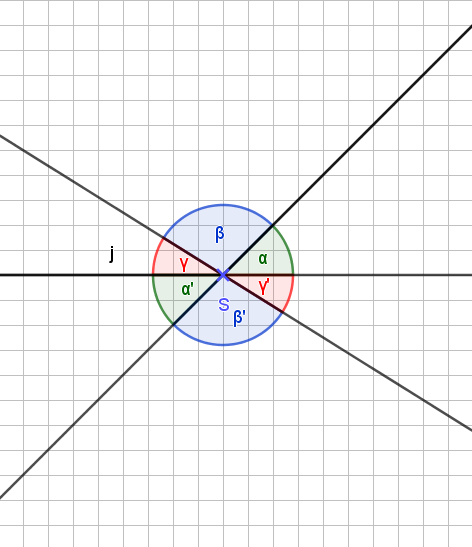
Es bleibt auch hier (fast) alles beim Alten
Super! Neu ist nur, dass wir nicht mit Nebenwinkeln arbeiten können. Wir erkennen aber: Jeweils drei (bei mehr Geraden entsprechend der Anzahl der sich schneidenden Geraden) nebeneinanderliegende Winkel ergänzen sich zu 180°.
Also z.B.:
α + β + γ = 180°
oder
β + γ + α‘ = 180°
oder…
Führen wir das Ganze noch ein wenig fort und lassen eine Gerade jetzt zwei Parallelen schneiden. Auch hier gibt es ein paar nützliche Beziehungen, nämlich zunächst die
Bei den nun acht vorhandenen Winkeln an beiden Scnittpunkten greifen wir uns der Übersichtlichkeit halber einzelne Gruppen heraus.
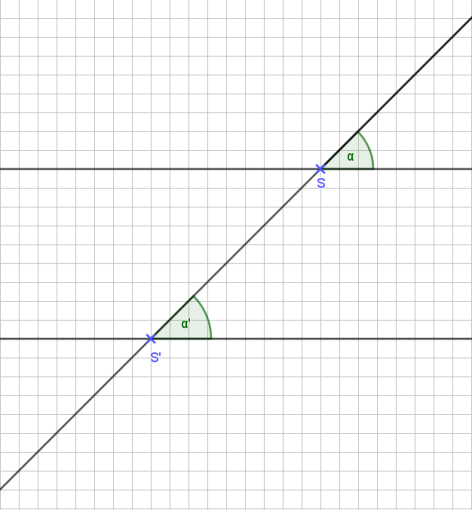
Nehmen wir α und α‘. Beide sind gleich groß, da die Gerade ja beide Parallelen unter dem gleichen Winkel schneidet. Da die beiden Winkel sozusagen wie auf Treppenstufen oben aufliegen, nennen wir sie Stufenwinkel. Es gilt:
Stufenwinkel sind gleich groß.
Oder:
α = α‘
Natürlich sind dann auch β und β‘ Stufenwinkel und gleich groß.
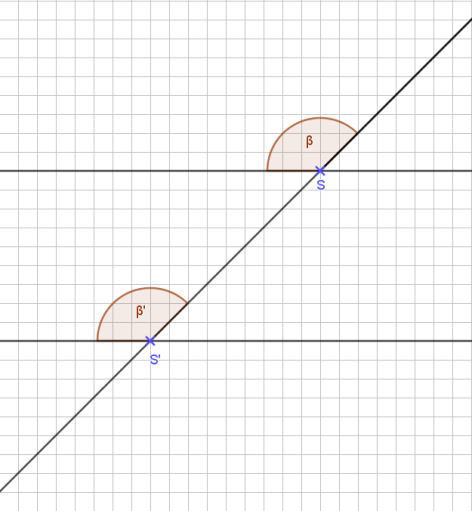
Es gibt aber noch ein anderes Winkelpaar, das von Interesse ist, nämlich die
Schauen wir uns das an:
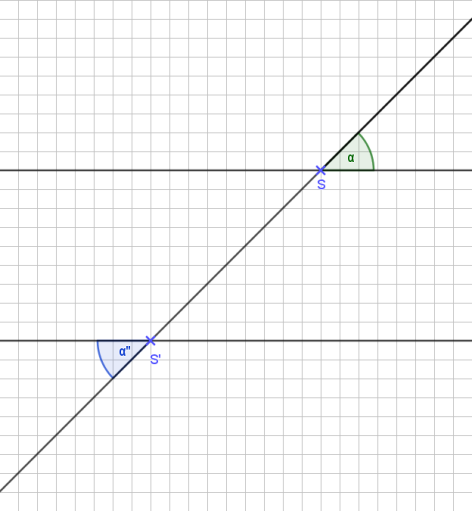
Das Winkelpaar α und α‘‘ nenne wir Wechselwinkel, weil sie wechselseitig von den Parallelen liegen. Wir sehen auch hier:
α = α‘‘
Damit gilt:
Wechselwinkel sind gleich groß.
Wir sehen, das ist nicht wirklich schwer, wir müssen uns nur ein paar Begrifflichkeiten merken.
Können wir auch etwas damit anfangen? Aber sicher doch. Außer dem Berechnen fehlender Winkel können wir damit auch die Winkelsumme im Dreieck bestimmen. Das könnt Ihrhier nachlesen.