Exponentielles Wachstum

Die Weizenkornlegende

Dieses Kapitel möchte ich mit einer Legende beginnen:
"Der indische Herrscher Shihram tyrannisierte seine Untertanen und stürzte sein Land in Not und Elend. Um die Aufmerksamkeit des Königs auf seine Fehler zu lenken, ohne seinen Zorn zu entfachen, schuf Dahirs Sohn, der weise Brahmane Sissa, ein Spiel, in dem der König als wichtigste Figur ohne Hilfe anderer Figuren und Bauern nichts ausrichten kann. Der Unterricht im Schachspiel machte auf Shihram einen starken Eindruck. Er wurde milder und ließ das Schachspiel verbreiten, damit alle davon Kenntnis nähmen. Um sich für die anschauliche Lehre von Lebensweisheit und zugleich Unterhaltung zu bedanken, gewährte er dem Brahmanen einen freien Wunsch. Dieser wünschte sich Weizenkörner: Auf das erste Feld eines Schachbretts wollte er ein Korn, auf das zweite Feld das Doppelte, also zwei, auf das dritte wiederum die doppelte Menge, also vier und so weiter. Der König lachte und war gleichzeitig erbost über die vermeintliche Bescheidenheit des Brahmanen.
Als sich Shihram einige Tage später erkundigte, ob Sissa seine Belohnung in Empfang genommen habe, musste er hören, dass die Rechenmeister die erforderliche Menge der Weizenkörner noch gar nicht fertig berechnet hätten. Der Vorsteher der Kornkammer meldete nach mehreren Tagen ununterbrochener Arbeit, dass so viel Weizen im ganzen Reich nicht aufgebracht werden könne..." (Quelle: WikipediaWeizenkornlegende) Wenn wir die Anzahl wirklich genau berechnen könnten, ergäbe das so viel Weizenkörner, dass die gesamte (!) Erdoberfläche mit einer mehrere cm mächtigen Schicht aus Weizenkörnern bedeckt wäre.

Dieser Geschichte liegt ein Wachstum zugrunde, das sehr, sehr viel stärker ist als alles, was wir bislang kennengelernt haben. Woran liegt das? Nun, da müssen wir uns erst noch eimal daran erinnern, was eine Potenz eigentlich ist. Sie besteht ja zwei Teilen, nämlich Basis und Exponent. Die Basis bildet eine Zahl und der Exponent gibt an, wie oft die Zahl mit sich selbst multipliziert wird. Kompliziert? Schauen wir uns ein Beispiel an:

2⁵

Die Basis ist die 2, der Exponent die 5. Das heißt, die 2 muss fünfmal mit sich selbst multipliziert werden, um den Wert zu berechnen, also 2 · 2 · 2 · 2 · 2. Das Ergebnis ist dann 32. Durch das fortgesetzte multiplizieren mit dem gleichen Faktor werden sehr schnell sehr hohe Zahlen erreicht. Bei 2¹⁰ sind wir schon bei 1024, bei 2 · 10, wären wir erst bei 20 und selbst bei 10² (quadratisches Wachstum) sind wir erst bei 100. Schauen wir uns die drei Wachstumsarten zusammen in einem Schaubild an:.

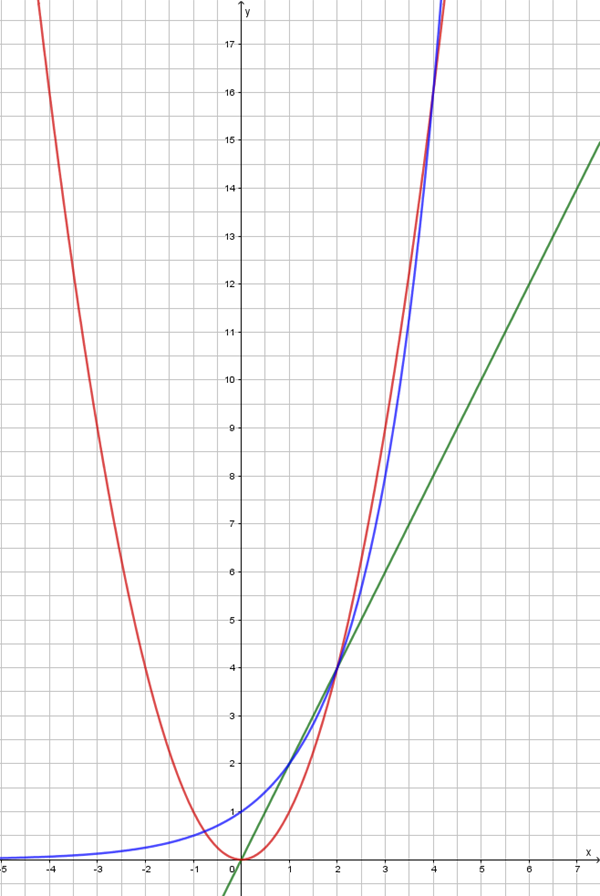
Die grüne Linie stellt den Zusammenhang \(~y = 2~x\) dar. Wir haben ein lineares Wachstum, das Schaubild ist eine gerade. Die rote Linie \((~y = x^2)\) zeigt quadratisches Wachstum an und die blaue Linie \((y = 2^x)\) das exponentielle.
Wir sehen, bis \(x = 2\) tut sich nicht allzu viel. Danach steigt erst die rote Linie stärker an, ab \(x = 4\) steigt die blaue Linie stärker an – und das bleibt dann auch so. Das heißt, eine nur Änderung beim x-Wert ergibt eine sehr hohe Änderung beim Funktionswert.

Berechnung exponentiellen Wachstums

Schauen wir uns nun an, wie wir exponentielles Wachstum berechnen können:

Zunächst brauchen wir einen Anfangswert \(N_0\), denn irgendetwas muss ja da sein, um wachsen zu können.
Dann brauchen wir noch den Wachstumsfaktor \(q\). Den erhalten wir, indem wir das geschehen über einen bestimmten Zeitraum – nehmen wir hier eine Woche – verfolgen.
Nehmen wir an, der Startwert beträgt 5.
Nach einer Woche habe ich 7.
Das Ganze ist also um 2 angestiegen oder um \(2 \over 5\) oder um 40% (p) oder um 0,4.
Den Wachstumsfaktor \(q\) bestimmen wir wie beim prozentualen Aufschlag bei der Berechnung von Bruttopreisen in der Prozentrechnung

Bei derProzentrechnung hatten wir ja bei der Berechnung der Bruttopreise einen Faktor von 1,19 (19% Umsatzsteuer) und konnten damit ausrechnen, womit wir den Nettopreis multiplizieren müssen. Nun haben wir aber kein Geld, sondern etwas ganz Beliebiges, das wachsen kann. Bei meinem Beispiel oben, haben wir 40% Wachstum und damit beträgt der Wachstumsfaktor \(q = 1,4\). Multiplizieren wir jetzt den Anfangswert mit \(q\) erhalten wir:

\[\large 5 \cdot 1,4 = 7\]

Super das stimmt. Jetzt haben wir 1 Woche erledigt. Wie sieht das aber nach 2, 3, 4… Wochen aus? Dazu haben wir noch einen Zeitfaktor \(t\). Dieser wird Exponent beim Wachstumsfaktor – denn jede Woche wächst das Ganze um den gleichen Faktor:

\[\large N = 5 \cdot 1,4 \cdot 1,4 \cdot 1,4 \cdot 1,4...\]

Unsere Formel ergänzt sich dann zu:

\[\large N = N_0 \cdot q^t\]

oder

\[\Large N = N_0 \cdot \left(1 + {p \over 100}\right)^t\]

Wollen wir in unserem Beispiel wissen, wie das nach 8 Wochen aussieht, setzen wir einfach alles ein:

\[\Large N = 5 \cdot \left(1 + {40 \over 100}\right)^8\]

Jetzt noch ein wenig den Taschenrechner quälen (Tipp: wer keinen Rechner mit sequenzieller Eingabe hat, erst die Klammer ausrechnen, dann potenzieren, dann mit dem Ausgangswert multiplizieren) und wir erhalten:

\[\large N = 5 \cdot 1,4^8 \approx 73,79\]

Ist das wieder nur pure Mathematik – oder ist das nützlich? Wie so oft im Leben – ist das natürlich nützlich. Dazu zwei Beispiele:

Infektionsgeschehen

Beim Infektionsgeschehen machen wir ein paar Vereinfachungen. Wir gehen davon aus, dass die Leute nicht gesunden oder gar sterben. Alles andere wird nämlich ein wenig komplizierter. Im Zuge des aktuellen Infektionsgeschehens, fällt oft der Begriff \(R\)-Wert. Das ist nichts anderes als der Term p/100 in unserer Formel. Er gibt an, wieviel Personen innerhalb einer Woche von einer Person angesteckt werden. Rechnen wir einmal zwei Beispiel durch. Die Frage ist, wieviel Infizierte haben wir nach 5 Wochen, wenn wir am Anfang 1000 Infizierte haben? Im ersten Fall liegt der \(R\)-Wert bei 0,6, im zweiten bei 1,4.
Im ersten Fall erhalte ich nach 5 Wochen:

\[\large N = 1000 \cdot (1 + 0,6)^5 \approx 10485,76~ \text{Infizierte}\]

Und im zweiten Fall:

\[\large N = 1000 \cdot (1 + 1,4)^5 \approx 79626,24~ \text{Infizierte}\]

Wie wir sehen, ist der Unterschied enorm. Daher bemüht man sich durch verschiedene Maßnahmen, den \(R\)-Wert möglichst klein zu halten.

Zinseszinsrechnung

Über Zinsrechnung haben wir ja schon Einiges gehört. Aber was passiert, wenn die erhaltenen Zinsen, dem Ausgangskapital gutgeschrieben werden und im nächsten Schritt mitverzinst werden? Dann nennen wir das Ganze Zinseszinsrechnung und sind wieder beim exponentiellen Wachstum. Wir tauschen nur ein paar Begriffe aus und sind schon fertig. Aus der Anzahl \(N\) wird das Kapital \(K\). Aus dem Anfangswert \(N_0\) wird das Startkapital \(K_0\). Schon sind wir fertig! 😊
Unsere Wachstumsformel ändert sich zur Zinseszinsformel:

\[\Large K = K_0 \cdot \left(1 + {p \over 100} \right)^t\]

Auch hier ein Beispiel:
Auf welchen Wert wächst ein Startkapital von 1200 €, wenn es für 10 Jahre angelegt wird und jährlich 1,1% Zinsen bringt? Die Zinsen werden mitverzinst.
Okay, setzen wir ein:

\[\Large K = 1200 \cdot \left(1 + {1,1 \over 100} \right)^{10} \approx 13338,73\]

Super, ist doch gar nicht so schwer!

Natürlich können wir – und eure Mathelehrer werden davon sicher Gebrauch machen 😉 – die Formel auch umstellen und anstatt \(K\) (oder \(N\)) dann \(K_0\) (oder \(N_0\)) ausrechen. Dann sieht die Formel folgendermaßen aus:

\[\Large K_0 = {K \over {\left(1 + {p \over 100}\right)^t}}\]

Auch \(p\) oder \(t\) kann man ausrechnen, braucht dazu aber noch andere, fortgeschrittene Rechentechniken, die zuallermeist an dieser Stelle nicht im Unterricht behandelt werden. Daher gehe ich hier nicht darauf ein. Dafür habe ich euch aber wieder eine Möglichkeit geschaffen, eure Rechnungen zu überprüfen.

Bitte beachten:

Javascript darf nicht deaktiviert sein.
Bei Kommazahlen bitte einen Punkt statt Komma eingeben.
Alle Ergebnisse sind auf zwei Stellen nach dem Komma gerundet.