Das folgende Kapitel soll einen ersten Einblick in die Welt der Vektoren geben.
In den Naturwissenschaften stolpern wir sehr häufig über sogenannte Vektoren. Klassischerweise sind die ersten Berührungen damit in der Physik bei der Behandlung von Kräften. Wir erinnern uns (hoffentlich 😉): Kräfte können wir nicht sehen, sondern nur an ihren Wirkungen erkennen. Wenn jetzt also eine Kraft einen Gegenstand bewegen soll, muss ich wissen, in welcheRichtung der Gegenstand bewegt werden soll und wie groß die Kraft sein muss, um das zu bewirken. Die Größe der Kraft nennen wirBetrag. Und zuletzt müssen wir noch wissen, an welchemAngriffspunkt die Kraft wirken soll. Mit diesen drei Größen ist das Ereignis definiert. Okay… Wie sieht das aus, wenn wir das mathematisch konkret betrachten?
Vektoren sind schlicht und einfach Strecken bestimmter Länge (Betrag ), die eine bestimmteRichtung haben. Unter Umständen ist es auch sinnvoll, einen gegebenenAusgangspunkt vorzugeben. Wichtig ist, dass in der Mathematik der Vektornur überBetrag undRichtung definiert ist. Das heißt, die Lage im Koordinatensystem ist letztlich völlig egal! Nur zum Zeichnen des Vektors brauche ich zwei Punkte, um Betrag und Richtung zu definieren. Kompliziert? Okay schauen wir uns das praktisch im Koordinatensystem an:
Wir haben einen Punkt A mit den Koordinaten A (3 | 2).
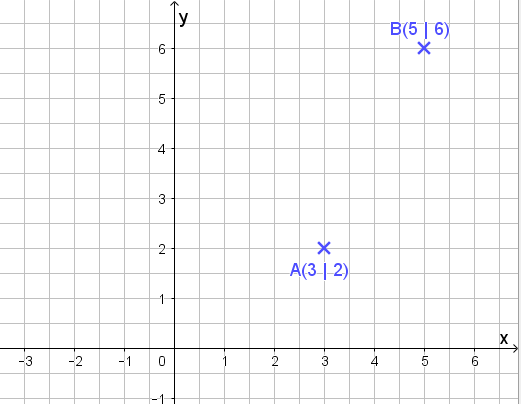
Die Richtung wird über einen zweiten Punkt B festgelegt mit B (5 | 6).
Jetzt zeichnen wir einen Pfeil, der bei A beginnt und bei B endet.
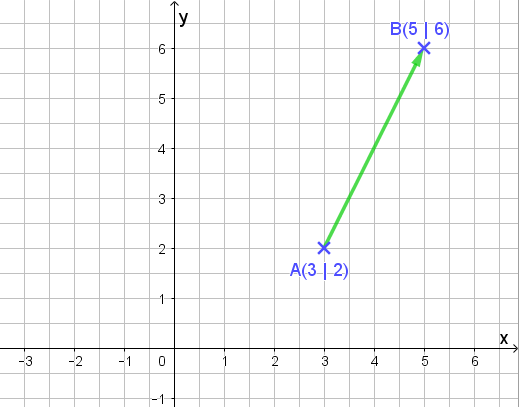
Fertig ist der Vektor. Die Richtung wird einfach mit der Pfeilspitze gekennzeichnet.
Noch einmal etwas anders:
um einen Vektor zu zeichnen brauche ich zwei Punkte. Der erste Punkt bestimmt den Anfang des Vektors. Die Richtung wird durch den zweiten Punkt bestimmt. Die Länge des Vektors ist dann der Betrag des Vektors. Damit haben wir im Übrigen aus unserem Physikbeispiel auch alle Komponenten untergebracht. Kommen wir nach der ersten Definition nun zur mathematischen
Das Symbol für Vektoren ist in der Mathematik heute ein kleiner lateinischer Buchstabe, über dem ein kleiner Pfeil (nach rechts gerichtet) gezeichnet ist (früher waren es altdeutsche Buchstaben – auch international!). Also z.B.
\[\vec {u} \]Das ist nicht sonderlich schwer… 😉. Aber wie gebe ich jetzt die Richtung an? Ganz einfach. Das funktioniert so ähnlich, wie bei derBestimmung einer Geradensteigung aus dem Graphen. Wir müssen überlegen: wie komme ich von Punkt A über rechte Winkel zu Punkt B?
Nehmen wir unser obiges Beispiel:
A hatte die Koordinaten A (3 | 2), B die Koordinaten (5 | 6). Zuerst nehmen wir die x-Richtung. Ich muss zwei Einheiten nach rechts gehen, um auf die Höhe von B zu kommen. Danach muss ich vier Einheiten senkrecht nach oben gehen, um B zu treffen.
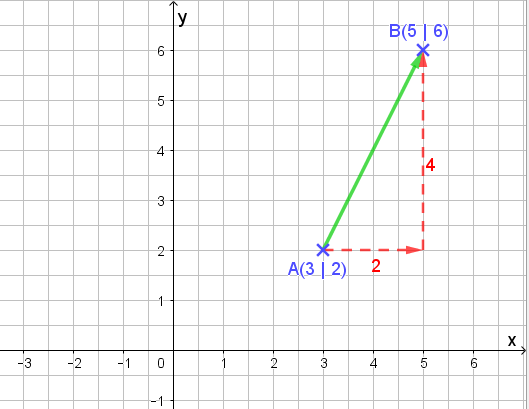
Genau das setzen wir in einer speziellen Schreibweise um, und zwar in die Spalten-Schreibweise:
\[\vec{u}=\begin{pmatrix} 2 \\4 \end{pmatrix}\]
Oben steht die x-Komponente, unten die y-Komponente. Die Schreibweise ist auch sehr praktisch; denn ein Vektor hat, wie ich oben schon geschrieben habe, nur eine relative Position. Egal, wo der Vektor im Koordinatensystem liegt, ich kann ihn immer auf die gleiche Weise konstruieren: ich nehme einen Punkt, gehe zwei nach rechts und vier senkrecht nach oben.
Rechnerisch erhalte ich den Vektor, wenn ich vomZielpunkt (hier: B) die jeweiligen Komponenten (x und y) desStartpunktes subtrahiere. Die Reihenfolge ist wichtig, weil ich sonst eine andere Richtung bekomme.
\[\vec{u}=\begin{pmatrix} {5-3} \\{6-2} \end{pmatrix}=\begin{pmatrix} 2 \\4 \end{pmatrix}\]
Okay, das ist nicht so kompliziert. Wenden wir uns jetzt zu dem
Zeichne den Vektor
\[\vec{v}=\begin{pmatrix} 3 \\1 \end{pmatrix}\]
Okay… Ich markiere mir einen Punkt (hier A (1 | 1) ).
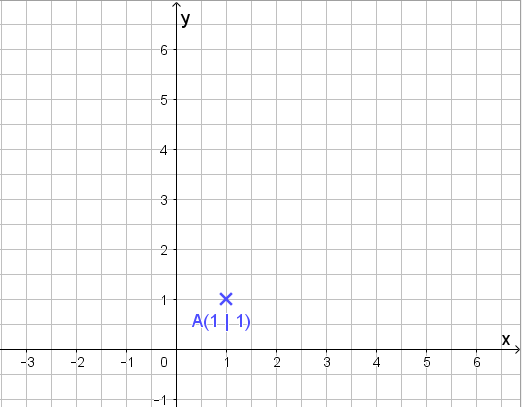
Nun gehe ich drei nach rechts und eins nach oben. Dort erhalte ich B:
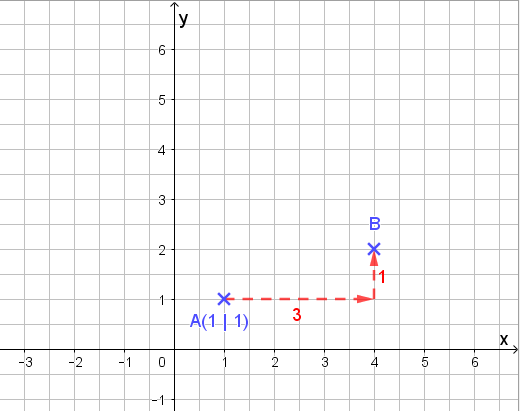
Nun verbinde ich die beiden und zeichne die Pfeilspitze ein:
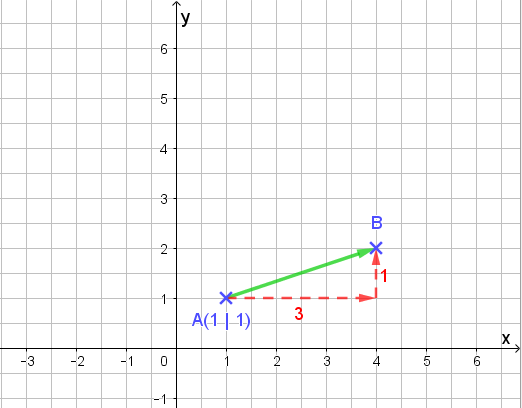
Fertig! 😊 Und auch mit negativen Zahlen bei der Richtung haben wir keine Probleme. Wie bei der Steigungsbestimmung gehen wir bei negativen Zahlen in der x-Komponente nach links und bei negativen Zahlen in der y-Komponente nach unten. Auch das zeigen wir gleich an einem Beispiel.
Zeichne den Vektor
\[\vec{w}=\begin{pmatrix} -2 \\-3 \end{pmatrix}\]
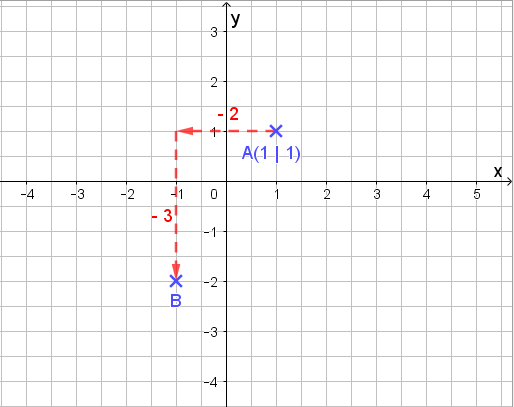
Okay… Ich markiere mir einen Punkt (hier A (1 | 1) ).
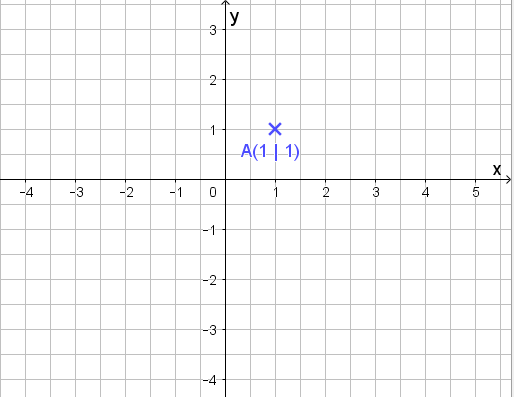
Nun gehe ich zwei nach links und drei nach unten. Dort erhalte ich B:
Nun verbinde ich die beiden und zeichne die Pfeilspitze ein:
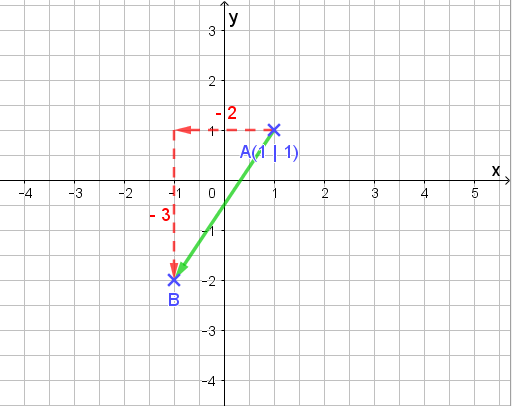
Ist doch gar nicht so schwer…
Zum Schluss setzen wir noch einen drauf 😉 Die meisten Prozesse finden ja nicht in der Ebene statt, sondern im Raum. Gerade hier kann man sehr gut mit Vektoren arbeiten. Allerdings brauchen wir dann eine Angabe mehr, da wir ja in x-, y- und z-Richtung arbeiten. Wenn wir also vom Punkt A (2 | 4 | – 3) aus einen Vektor zum Punkt B (-4 | -2 | 5) zeichnen wollen, machen wir das ganz genauso, wie in der Ebene. Wir erhalten dann den Vektor
\[\vec{u}=\begin{pmatrix} {-4-2} \\ {-2-4} \\ {5-(-3)} \end{pmatrix}=\begin{pmatrix} -6 \\ -6 \\ 8\end{pmatrix}\]Räumlich sieht die Lösung folgendermaßen aus (rot: x-Achse, grün: y-Achse und blau: z-Achse):
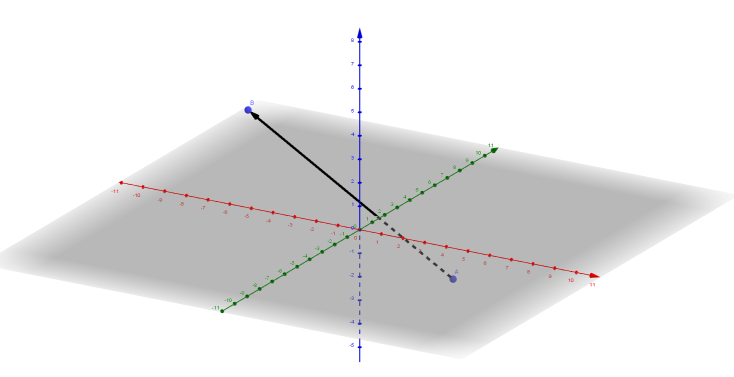
Jetzt taucht nur die Frage auf: Warum das Ganze? Nun, wir haben in den Naturwissenschaften sehr viele gerichtete Größen, nicht nur Kräfte. Und mit Hilfe der Vektorrechnung kann man sehr gut mit diesen Größen arbeiten, und zwar sehr viel eleganter und schneller, als wenn wir herkömmlich damit arbeiten müssten. Vektoren machen einem das Leben hier viel leichter 😊. Glaubt es mir, ich habe im Studium sehr viel damit zu tun gehabt…
So, nach dieser kleinen Einführung sind wir fit für die Addition und Subtraktion von Vektoren.