Wie bestimme ich die Gleichung einer unbekannten Geraden?

Hmmm… Ich habe nur eine Gerade im Koordinatensystem, aber sonst keine Angaben… Kann ich denn trotzdem die Geradengleichung herausfinden?
Klar geht das! Das ist im Prinzip so, wie Geraden mit Punkt und Steigung zeichnen, nur umgekehrt. Hört sich jetzt nicht soo schwierig an? Ist es auch nicht. Gehen wir in zwei Schritten vor und betrachten zunächst nur:

Geraden durch den Nullpunkt

Solche Geraden werden durch die allgemeine Gleichung \(\boldsymbol {y = m~x}\) dargestellt. Aus dem Graphen kann ich zunächst direkt erkennen, ob die Steigung \(~m\) positiv oder negativ ist. Entscheidend ist der Winkel, den die Gerade mit der \(x\)-Achse bildet. Ist er kleiner als 90°, ist die Steigung positiv, ist er größer als 90°, ist die Steigung negativ. Okay, das hilft ja schon mal weiter - und ganz ohne Rechnen... 😊 Danach wähle ich einen Punkt \(P_1\) auf der Geraden. Von diesem aus trage ich eine Strecke parallel zur \(x\)-Achse ab. Am Endpunkt der Strecke zeichne ich senkrecht zur gezeichneten Strecke eine zweite Strecke, die wieder auf der Geraden in \(~P_2\) endet. Jetzt bestimme ich die Längen beider Strecken. Im Anschluss dividiere ich den Wert der Strecke, die parallele zur \(y\)-Achse verläuft durch den Wert der Strecke, die parallel zur \(x\)-Achse verläuft. Das Ergebnis ist die Steigungm. Fertig! Ein bisschen zu abstrakt? Keine Angst!!! Hier kommt noch Anschauungsmaterial:

Beispiel 1

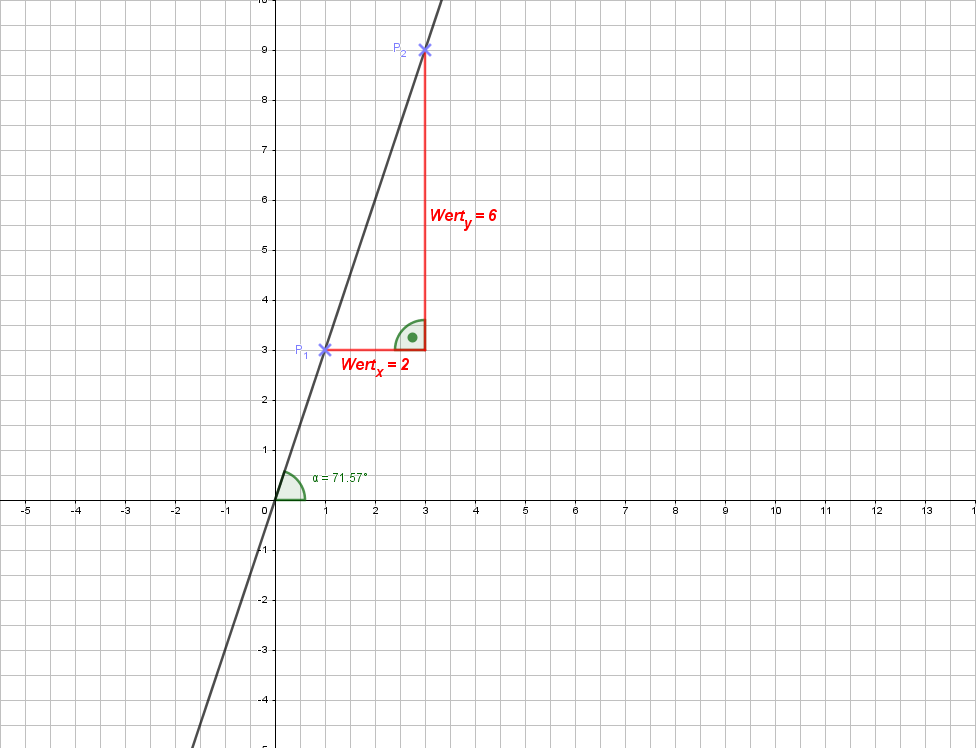
Die Steigung ist positiv. Der Wert der Strecke iny-Richtung beträgt: 6, der inx-Richtung: 2. Damit ist die Steigung: \[\boldsymbol {m = {6 \over 2} = 3}\] Die Gerade verläuft durch den Nullpunkt (\(b = 0)\), damit ist Geradengleichung:

Beispiel 2:

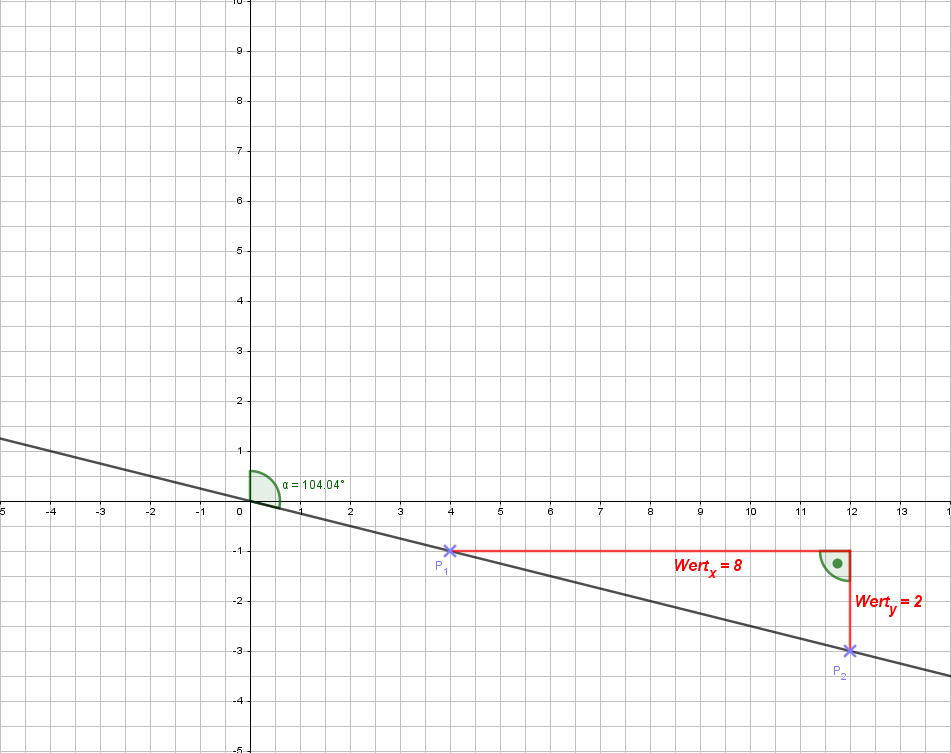
In diesem Fall liegt eine negative Steigung vor und \(~m\) bekommt damit ein negatives Vorzeichen. Ich gehe wieder so vor, wie eben gerade. Der Wert der Strecke in \(y\)-Richtung beträgt 2, der in \(x\)-Richtung 8. Damit ist die Steigung:

Die Gerade verläuft durch den Nullpunkt, damit ist Geradengleichung:

Das lief doch alles ganz glatt. Kommen wir nun zu den:

Geraden, die nicht durch den Nullpunkt laufen

Solche Geraden werden durch die allgemeine Gleichung \(y = m~x + b\) dargestellt. In diesen Fällen müssen wir zwei Schritte machen.
Im ersten Schritt schauen wir, wo der Graph die \(y\)-Achse schneidet. Das ist dann nämlich \(b\), wie wir beim Zeichnen von Geraden schon gelernt haben.
Im zweiten Schritt arbeiten wir wieder wie eben gerade: Ich wähle wieder einen Punkt \(P_1\) auf der Geraden. Von diesem aus trage ich eine Strecke parallel zur \(x\)-Achse ab. Am Endpunkt der Strecke zeichne ich senkrecht zur gezeichneten Strecke eine zweite Strecke, die wieder auf der Geraden in \(P_2\) endet. Jetzt bestimme ich die Längen beider Strecken. Im Anschluss dividiere ich den Wert der Strecke, die parallele zur \(y\)-Achse verläuft durch den Wert der Strecke die parallel zur \(x\)-Achse verläuft. Das Ergebnis ist die Steigung \(~m\). Jetzt muss ich nur noch die beiden ausgrechneten Werte in die allgemeine Geradengleichung einsetzen und bin - fertig! Auch hier noch zwei Beispiele, so dass der Kopf nicht zu rauchen braucht 😉

Beispiel 3

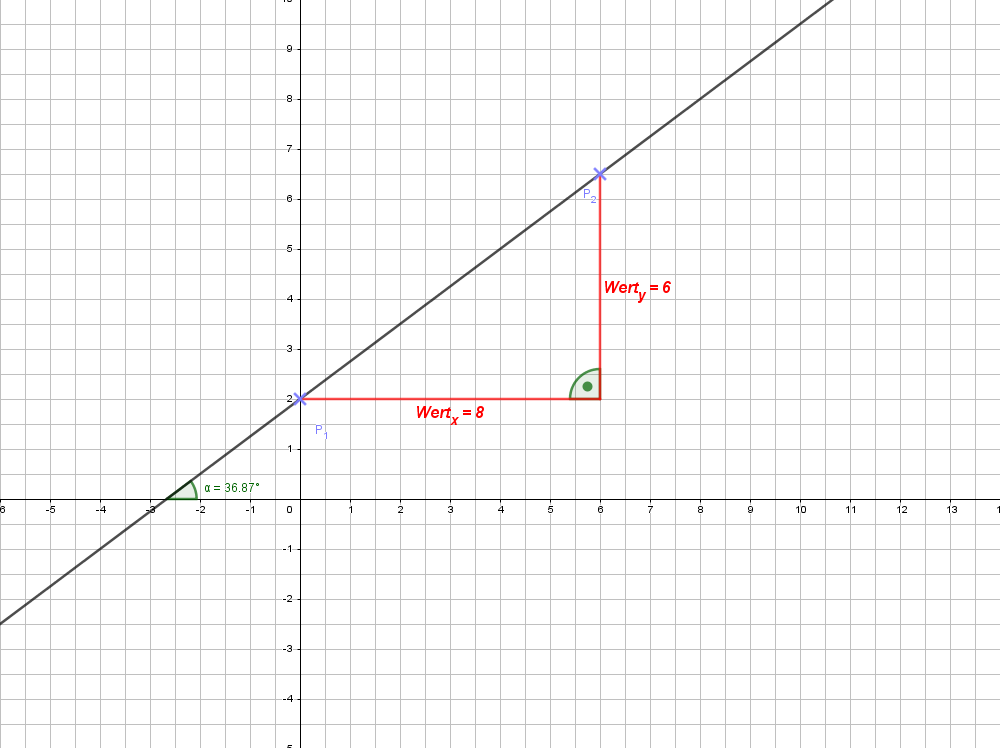
Die Gerade schneidet die \(y\)-Achse bei: + 2. Damit gilt: \(b = 2\).
Die Steigung ist positiv. Der Wert der Strecke in \(y\)-Richtung beträgt: 6, der in \(x\)-Richtung: 8. Damit ist die Steigung: \[\large{\boldsymbol{m = {6 \over 8} = {3 \over 4}}}\] Jetzt haben wir \(b\) und \(~m\). Damit lautet Geradengleichung:

Beispiel 4

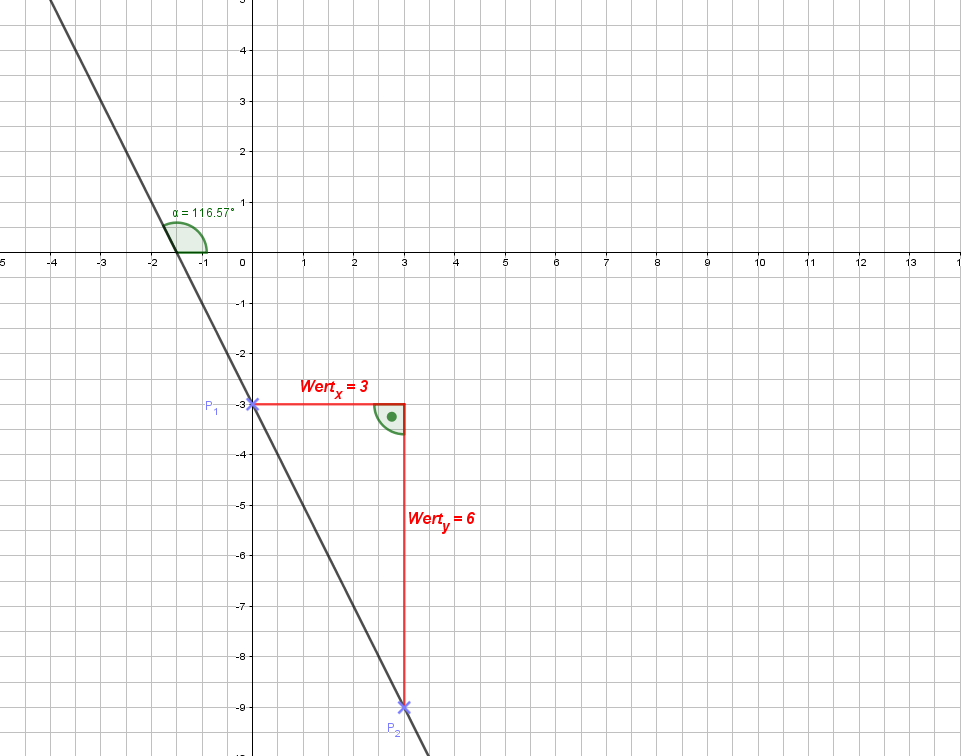
Die Gerade schneidet die \(y\)-Achse bei – 3. Damit gilt: \(b = - 3\). Die Steigung ist negativ. Der Wert der Strecke in \(y\)-Richtung beträgt: 6, der in \(x\)-Richtung: 3. Damit ist die Steigung:

Jetzt haben wir \(b\) und \(~m\). Damit lautet Geradengleichung:

Wir haben gesehen, es ist nicht schwer, eine Geradengleichung einfach aus dem Graphen zu entnehmen. Klasse, wie wir das hinbekommen haben! 😊😊