Dieses Kapitel wir wieder etwas umfangreicher, vor allem durch die Abbildungen. Wer einen gesuchten Punkt direkt anspringen möchte, ohne alles durchzuarbeiten, kann das hier tun:
Das ist eine gute Frage... Nun, da gibt es ganz schlaue Definitionen:
Hört sich nicht gut an? Okay, machen wir es anschaulicher:
Zwei Figuren sind genau dann kongruent, wenn ich sie nach dem Ausschneiden deckungsgleich (das heißt: nichts steht über, alles passt) aufeinanderlegen kann.
Mit dieser Definition könnt ihr euch den Wikipedia-Artikel wirklich ersparen...
Ich denke, das liest sich schon deutlich besser. 😉 Natürlich gilt die Definition von Kongruenz für alle Figuren, aber in der Mathematik benutzen wir die Kongruenz hauptsächlich bei Dreiecken, um zu beweisen, ob sie gleich sind. Das wollen wir hier nicht. Das Beweisen überlasse ich euren Mathelehrern. Bei mir geht es um die Anwendung des Ganzen (im Grunde um die Umkehrung). Uns interessiert die Frage, wie ich ein Dreieck aus drei gegebenen Stücken (es müssenimmer drei sein) eindeutig konstruieren kann. Dazu gibt es in der klassischen Geometrie vier verschiedene Möglichkeiten, die klassischen Kongruenzsätze. Wir kümmern uns in diesem Kapitel nur darum, wie wir nach diesen Sätzen ein Dreieck eindeutig konstruieren können.
Zwei Dreiecke sind dann kongruent, wenn sie in allen drei Seitenlängen übereinstimmen.
Also, wir haben die drei Seitenlängen gegeben - wie kriegen wir das Dreieck hin? Machen wir das am besten mit einem Beispiel - und das Schritt für Schritt:
Gegeben ist ein Dreieck mit a = 6 cm, b = 5 cm, c = 8 cm.
Vorgehen: Zuerst zeichnen wir die Seite c. Damit erhalten wir die PunkteA undB
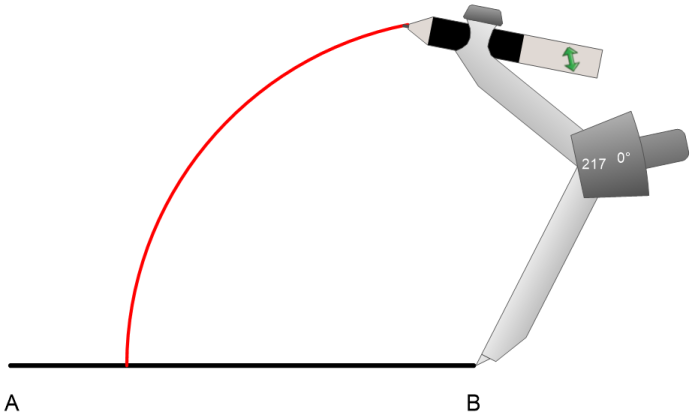
Danach nehmen wir einen Zirkel und stellen den Radius der Seite a (6 cm) ein.

Wir schlagen dann um PunktB einen Kreisbogen nach oben mit dem Radius der Seite a.
Nun nehmen wir einen Zirkel und stellen den Radius der Seite b (5 cm) ein.
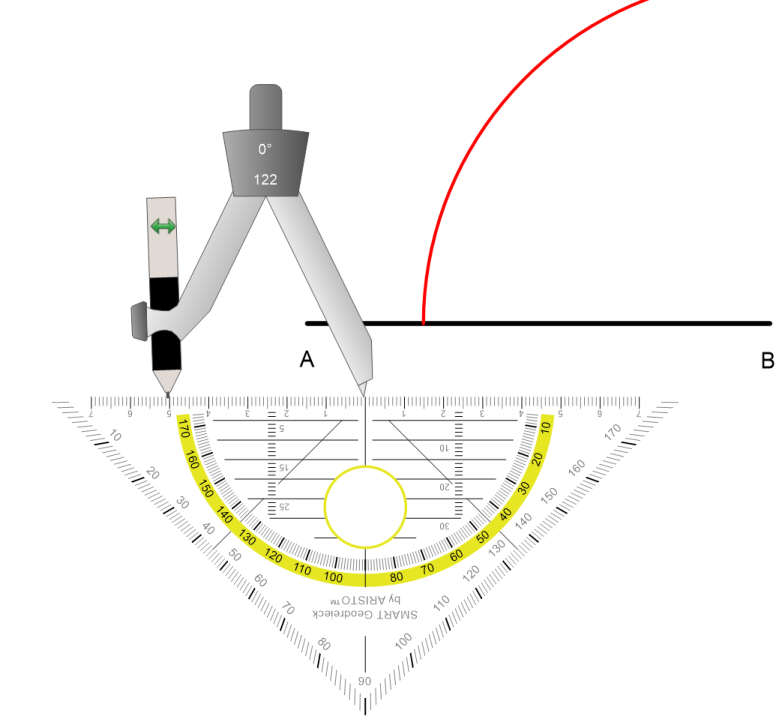
Danach schlagen wir um PunktA nach oben einen Kreisbogen mit dem Radius der Seite b.
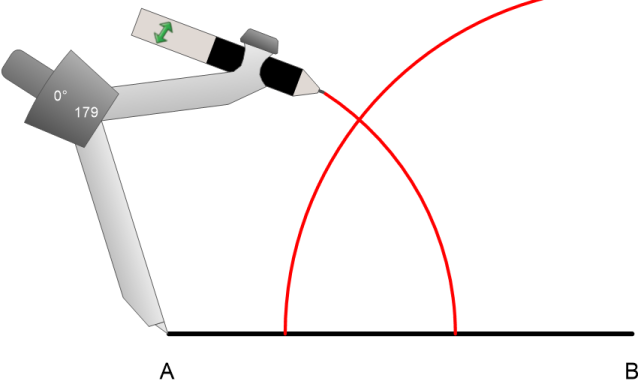
Wo die beiden Kreisbögen sich schneiden, liegt der PunktC.
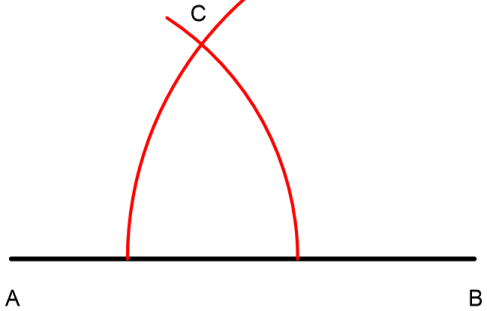
Jetzt verbinden wir noch die PunkteA undB mitC und erhalten das gesuchte Dreieck.
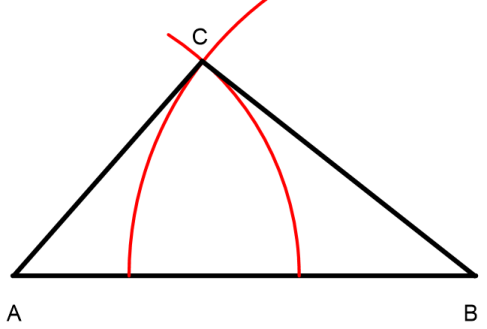
War doch gar nicht so schwer - oder?
Zwei Dreiecke sind dann kongruent, wenn sie in zwei Seitenlängen und dem von diesen Seiten gebildeten Winkel übereinstimmen.
Okay, nehmen wir uns auch hier ein Beispiel vor.
Gegeben ist ein Dreieck mit b = 5 cm, c = 8 cm, α = 55°
Vorgehen: Zuerst zeichnen wir die Seite c. Damit erhalten wir die PunkteA undB
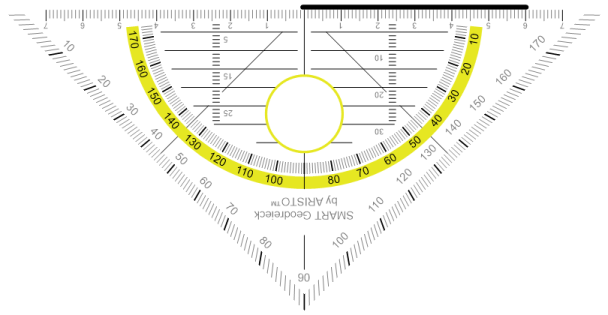
Als zweites zeichnen wir den Winkel α (55°).


Als drittes nehmen wir einen Zirkel und stellen den Radius der Seite b (5 cm) ein.

Danach schlagen wir um PunktA nach oben einen Kreisbogen mit dem Radius der Seite b.
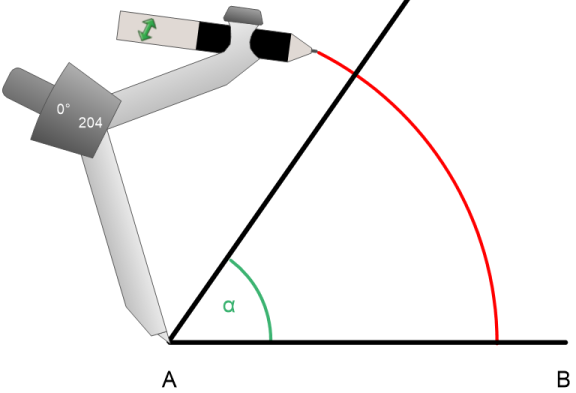
Dieser Kreisbogen schneidet den Schenkel des Winkels α im PunktC.
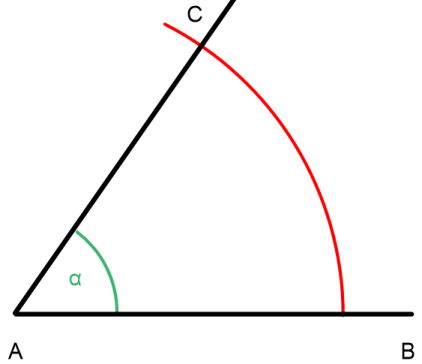
Jetzt verbinden wir noch den PunktB mitC und erhalten das gesuchte Dreieck.
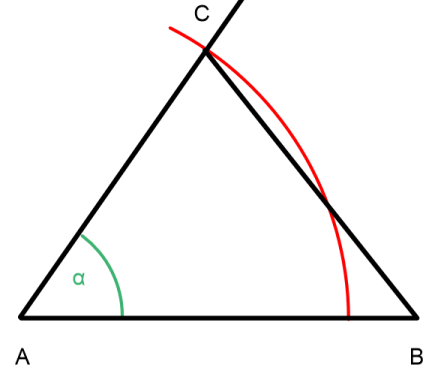
Ist doch machbar - oder? Ich finde es sogar noch ein wenig einfacher als bei SSS - aber das ist Geschmackssache... 😉
Zwei Dreiecke sind dann kongruent, wenn sie in einer Seitenlänge und den beiden Winkeln übereinstimmen, die an dieser Seite angrenzen.
Nun, auch hier hilft uns ein Beispiel. Das ist auch der einzige Satz, bei dem wir ohne Zirkel auskommen...
Gegeben ist ein Dreieck mit c = 6 cm, α = 55° und β = 30°.
Vorgehen: Zuerst zeichnen wir die Seite c. Damit erhalten wir die PunkteA undB
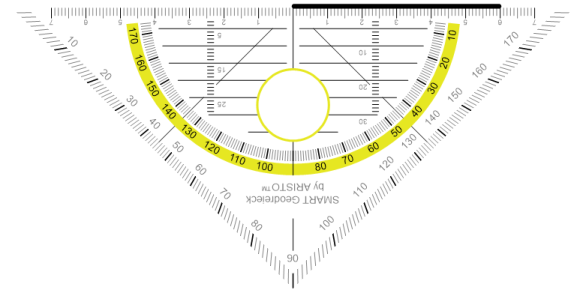
Als zweites zeichnen wir den Winkel α (55°).
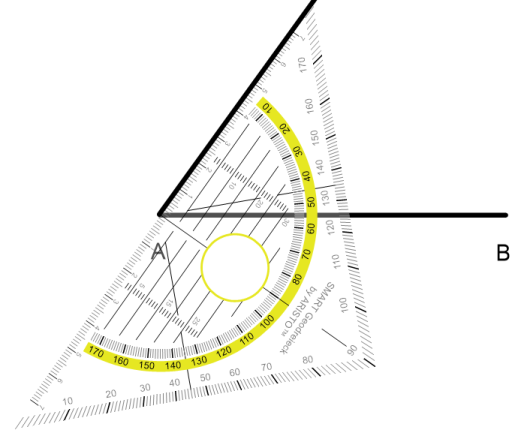
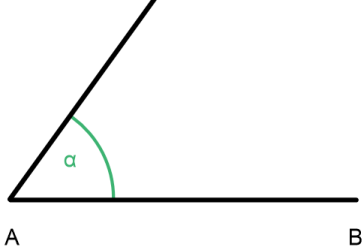
Als drittes zeichnen wir den Winkel β (30°)
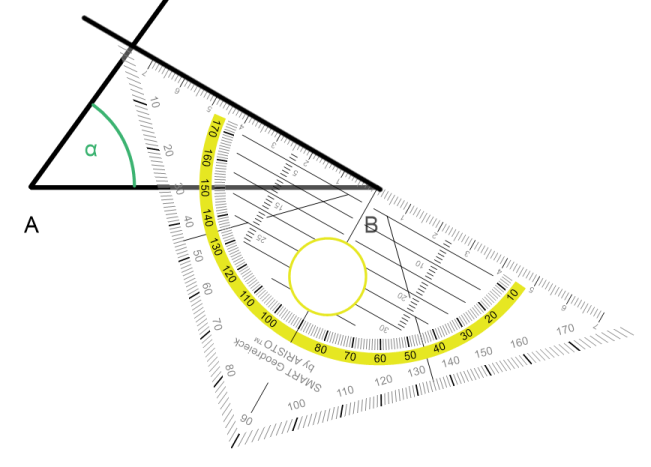
Die Schenkel der beiden Winkel schneiden sich im PunktC. So erhalten wir das gesuchte Dreieck.
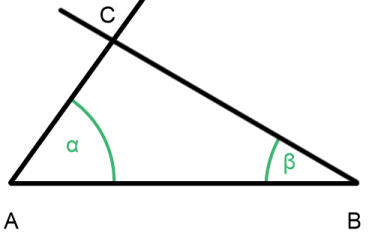
Auch das haben wir geschafft! Bei WSW haben wir auch die wenigsten Kostruktionsschritte... 😊
Zwei Dreiecke sind dann kongruent, wenn sie in zwei Seitenlängen übereinstimmen und dem Winkel, der der längeren Seite gegenüberliegt.
Auch beim letzten Satz nehmen wir uns gleich ein Beispiel vor.
Gegeben ist ein Dreieck mit a = 6 cm, c = 5 cm und α = 55°.
Vorgehen: Zuerst zeichnen wir die Seite c. Damit erhalten wir die PunkteA undB
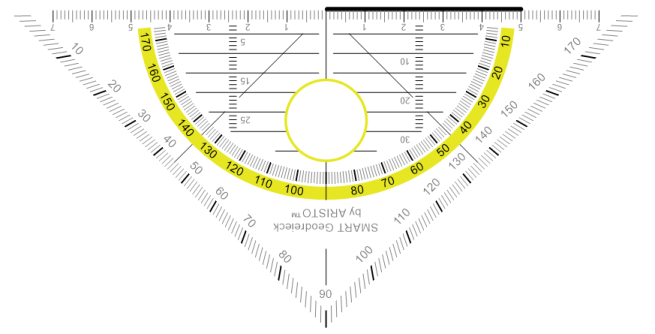
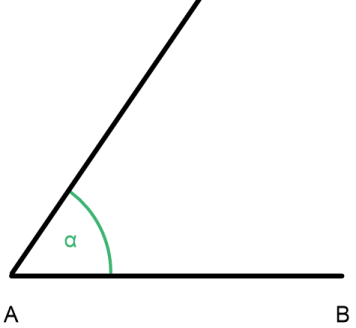
Als zweites zeichnen wir den Winkel a (55 °)
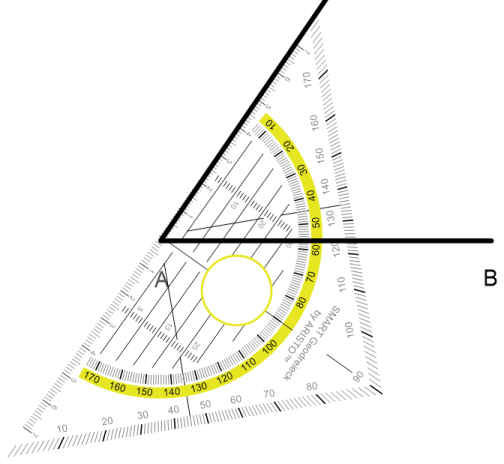
Als Drittes nehmen wir einen Zirkel und stellen den Radius der Seite a ein (6 cm).
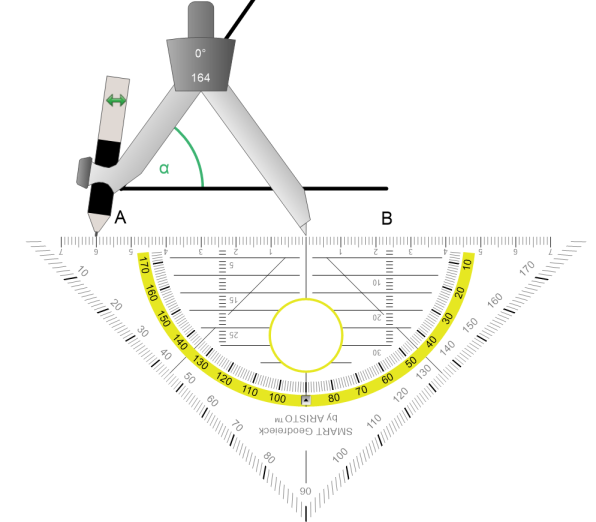
Danach schlagen wir um PunktB einen Kreisbogen mit dem Radius der Seite a.
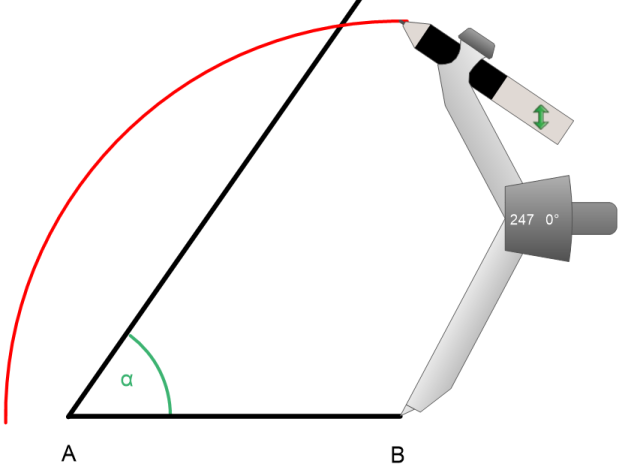
Der Kreisbogen schneidet den Schenkel des Winkels α und wir erhalten PunktC.
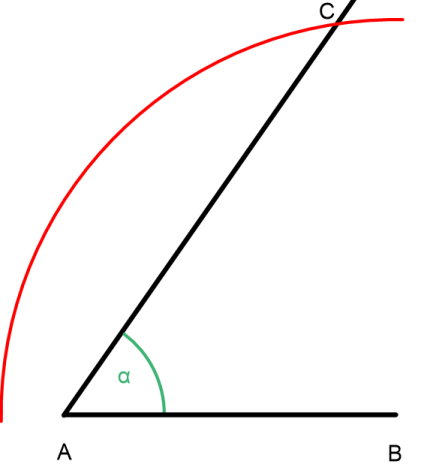
Jetzt verbinden wir nochB undC und erhalten das gesuchte Dreieck.
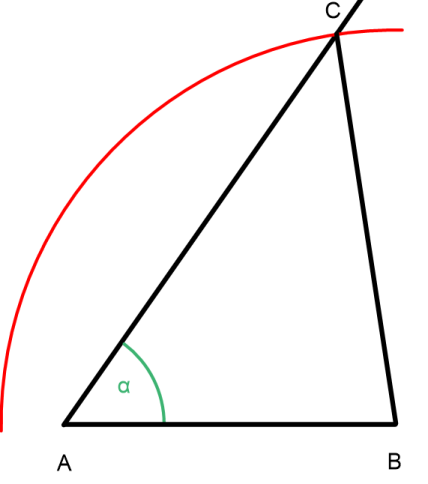
So, nun haben wir auch die Konstruktion nach dem letzten Satz geschafft! 😊 Bei der Konstruktion sollte auch klar geworden sein, warum es heißt: "...dem Winkel, der derlängeren Seite gegenüberliegt". Wäre es die kürzere Seite, könnte der Kreisbogen nicht den Schenkel des Winkels schneiden... Das wäre echt unpraktisch... 😉
Nach diesen Anleitungen lassen sich alle Konstruktionen nach den klassischen Kongruenzsätzen anfertigen. Das klappt auch wenn andere Seiten gegeben sind. Wir wissen ja schon aus dem Kapitel "Winkel am Dreieck zeichnen", dass wir dann darauf achten sollen, dass der PunktC wirklich oben liegt. Dann wird unser Vorstellungsvermögen bei den restlichen Schritten auch nicht so strapaziert.