Das ein Dreieck ein besonderes Teil ist, hast du sicher schon gemerkt. In diesem Kapitel wollen wir uns mit einer ganz speziellen Besonderheit der Figur beschäftigen. Es gibt nämlich besondere Linien mit besonderen Eigenschaften – und keine Angst! Das wird keine unendliche Geschichte… 😉 Es sind nur vier verschiedene Sorten. Ich werde euch erklären, wie man die zeichnen kann. Auch hier gibt es – wie meistens in der Mathematik – mehrere Möglichkeiten. Ich habe mir die für die entschieden, die meine Schülerinnen und Schüler in der Regel am praktischsten fanden. Zuerst erkläre ich jeweils, wie die besondere Linie heißt und wie sie im Dreieck verläuft. Dann zeige ich, wie man die Linie erzeugt und zuletzt gibt es noch Weiteres über die Linien zu lesen und ein paar interaktive Übungen.
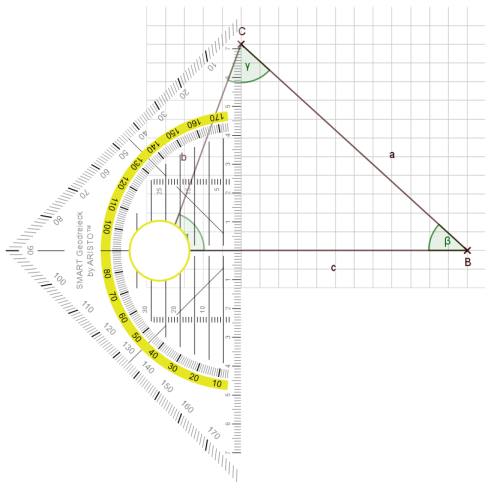
Eine Höhe steht senkrecht auf einer Seite und verläuft durch den gegenüberliegenden Punkt.
Konstruieren wir das Ganze mit dem Geodreieck:
Ich lege das Geodreieck mit der Nulllinie auf eine Seite. Dabei verschiebe ich es solange, bis ich den gegenüberliegenden Punkt treffe.

Dann zeichne ich eine Gerade durch diesen Punkt.
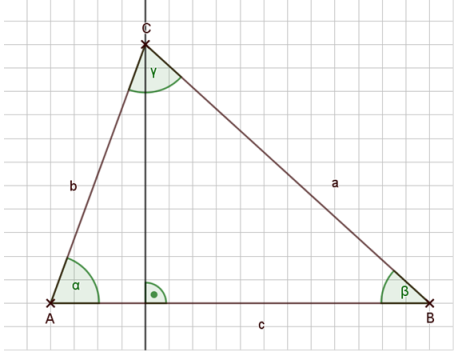
Wenn wir alle drei Höhen einzeichnen, stellen wir fest:
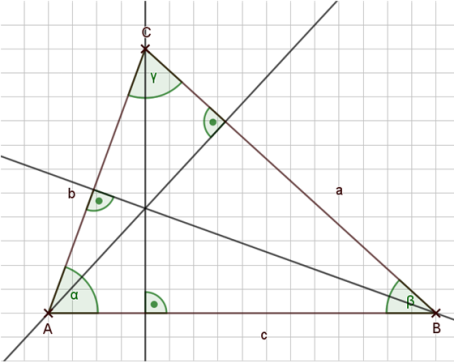
Alle drei Höhen im Dreieck schneiden sich in einem gemeinsamen Punkt. Dies ist der einzige Linienschnittpunkt, der keine besondere Bedeutung hat...
Eine Mittelsenkrechte verläuft senkrecht durch den Mittelpunkt einer Seite.
Zur Konstruktion könnte man auch hier das Geodreieck nehmen, aber mit dem Zirkel ist es einfacher. Ich zeige hier, wie man die Mittelsenkrechte zu einer Strecke erzeugt. Im Dreieck müssen wir das halt dreimal machen:
Gegeben ist eine StreckeAB.
Ich nehme einen Zirkel und stelle den Radius so ein, dass er größer ist als die Hälfte der Strecke und schlage einen Kreisbogen umA.
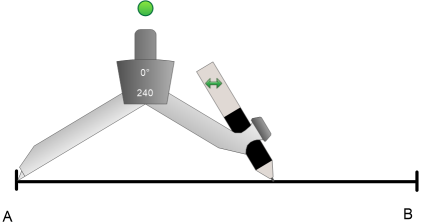
Anschließend schlage ich mit demselben (!) Radius einen Kreisbogen umB. Die beiden Kreisbögen schneiden sich zweimal.
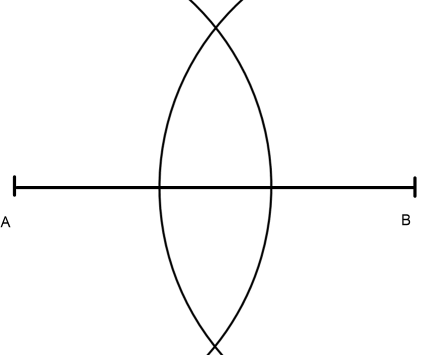
Anschließend zeichne ich eine Gerade durch die beiden Schnittpunkte. Diese Gerade ist die Mittelsenkrechte zur gegebenen Strecke.
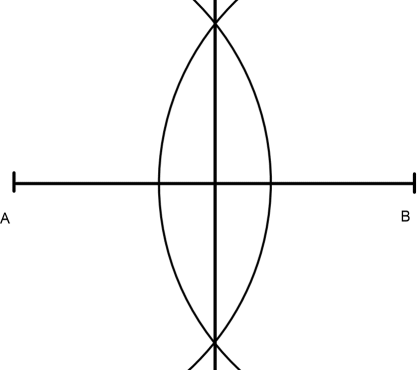
Im kompletten Dreieck sieht das dann folgendermaßen aus, wenn ich alle Mittelsenkrechte eingezeichnet habe:
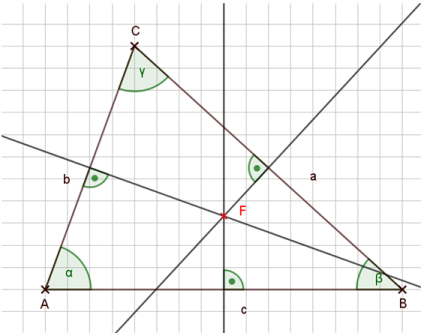
Wir sehen auch hier: Alle drei Mittelsenkrechten im Dreieck schneiden sich in einem gemeinsamen Punkt.
Dieser Punkt hat aber noch eine zusätzliche Besonderheit:
Der Schnittpunkt der Mittelsenkrechten im Dreieck ist der Mittelpunkt des Umkreises.
Das Ganze sieht dann so aus:
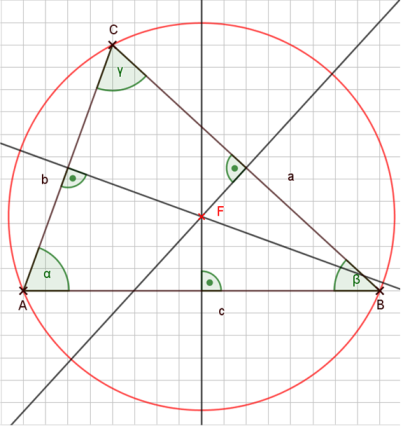
Eine Winkelhalbierende geht vom Scheitelpunkt eines Winkels aus und teilt den Winkel in zwei Hälften.
Auch hier nehmen wir besser den Zirkel:
Gegeben ist ein Winkel α.
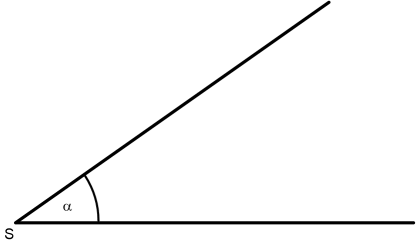
Ich nehme einen Zirkel und stelle einen beliebigen, nicht zu großen Radius ein. Ich schlage um S einen Kreisbogen und markiere nur die Schnittpunkte mit den Schenkeln.
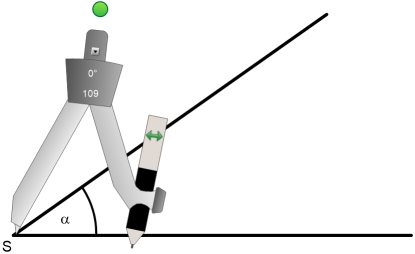
Ich schlage um diese beiden Schnittpunkte einen Kreisbogen mit demselben Radius.

Die beiden Kreisbögen schneiden sich dann im offenen Schenkel des Winkels.
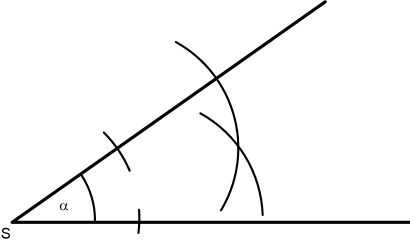
Nun zeichne ich einen Strahl von S ausgehend durch den Schnittpunkt der Kreisbögen. Das ist die Winkelhalbierende zum Winkel α.
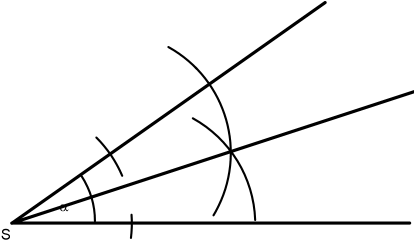
Im kompletten Dreieck sieht das dann folgendermaßen aus, wenn ich alle Winkelhalbierenden eingezeichnet habe:
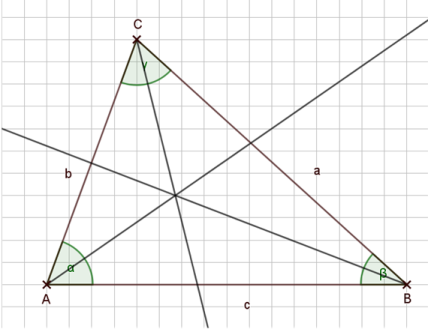
Wir sehen auch hier: Alle drei Winkelhalbierenden im Dreieck schneiden sich in einem gemeinsamen Punkt.
Dieser Punkt hat aber noch eine zusätzliche Besonderheit:
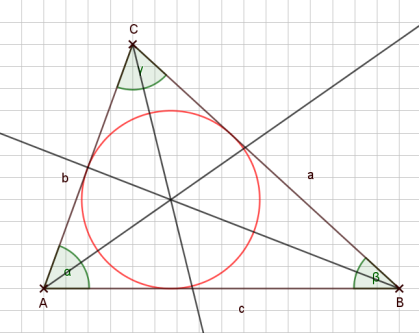
Der Schnittpunkt der Winkelhalbierenden im Dreieck ist der Mittelpunkt des Inkreises.
Das Ganze sieht dann so aus:
Eine Seitenhalbierende verläuft durch den Mittelpunkt einer Seite und den gegenüberliegenden Punkt.
Im Gegensatz zur Höhe muss die Seitenhalbierende also nicht zwangsläufig rechtwinklig auf der Seite stehen. Wenn sie es dennoch tut, sind Höhe und Seitenhalbierende für diese Seite identisch.
Bei dieser Konstruktion greifen wir wieder auf das Geodreieck zurück.
Ich lege das Geodreieck mit der Basis auf eine Seite. Dabei verschiebe ich es solange, bis ich den Mittelpunkt ermittelt habe und markiere ihn.
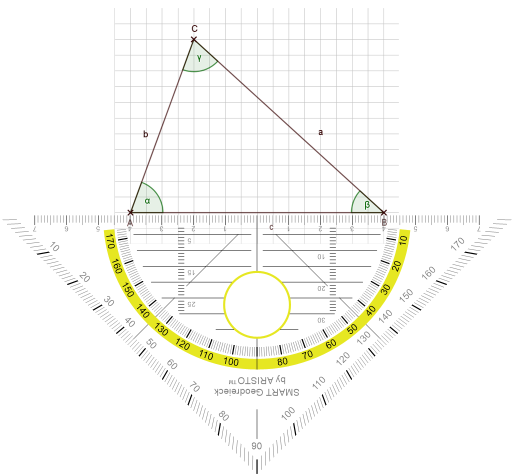
Dann zeichne ich eine Gerade durch den Mittelpunkt und den gegenüberliegenden Punkt.
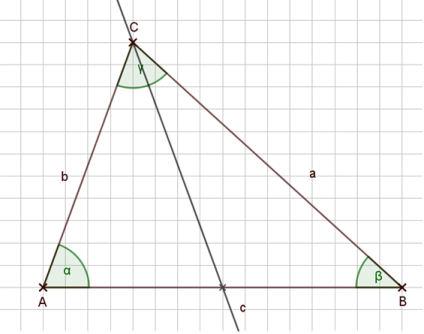
Im kompletten Dreieck sieht das dann folgendermaßen aus, wenn ich alle Seitenhalbierenden eingezeichnet habe:
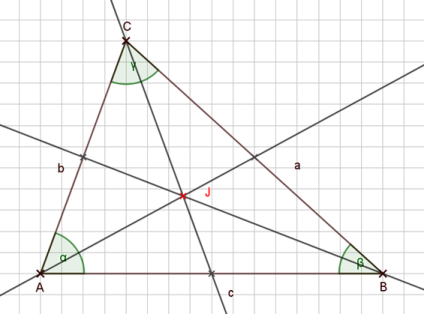
Wir sehen auch hier: Alle drei Seitenhalbierenden im Dreieck schneiden sich in einem gemeinsamen Punkt.
Dieser Punkt hat aber noch eine zusätzliche Besonderheit:
Der Schnittpunkt der Seitenhalbierenden im Dreieck ist der Schwerpunkt des Dreiecks.
Was bedeutet das? Ganz einfach: Schneiden wir das Dreieck mit den eingezeichneten Seitenhalbierenden sorgfältig aus, dann können wir das ausgeschnittene Dreieck mit dem Schnittpunkt auf eine Bleistiftspitze legen – es fällt dann nicht herunter - zumindest dann, wenn deine Hand entsprechend ruhig ist 😉.
Nun haben wir die vier besonderen Linien im Dreieck kennengelernt. Ich fasse das zur Übersicht nochmal in einer Tabelle zusammen
| Name der Linie | Verlauf | Bedeutung des Schnittpunkts |
|---|---|---|
| Höhe | Eine Höhe steht senkrecht auf einer Seite und verläuft durch den gegenüberliegenden Punkt. | keine |
| Mittelsenkrechte | Eine Mittelsenkrechte verläuft senkrecht durch den Mittelpunkt einer Seite. | Der Schnittpunkt der Mittelsenkrechten im Dreieck ist der Mittelpunkt des Umkreises. |
| Winkelhalbierende | Eine Winkelhalbierende geht vom Scheitelpunkt eines Winkels aus und teilt den Winkel in zwei Hälften. | Der Schnittpunkt der Winkelhalbierenden im Dreieck ist der Mittelpunkt des Inkreises. |
| Seitenhalbierende | Eine Seitenhalbierende verläuft durch den Mittelpunkt einer Seite und den gegenüberliegenden Punkt. | Der Schnittpunkt der Seitenhalbierenden im Dreieck ist der Schwerpunkt des Dreiecks. |
Im folgenden habe ich euch noch ein paar Geogebra-Arbeitsblätter fertig gemacht. Mit denen könnt ihr euch ein wenig mit dem Verhalten der einzelnen Linien beschäftigen und vielleicht auch das eine oder andere zusätzlich herausfinden. Eine Anleitung dazu ist jeweils vorhanden. Viel Spaß damit!