Ich weiß, viele Mathelehrer sehen hier immer noch den Einheitskreis und versuchen das Ganze daran aufzuarbeiten. Ich werde jedoch darauf verzichten und das Ganze pragmatisch angehen.
Zunächst ganz wichtig:
Greifen wir doch einmal auf unsere Vorkenntnisse zurück, nämlich zum einem zum Thema Ähnlichkeit:
Zwei Figuren sind genau dann ähnlich wenn sie
Zum anderen brauchen wir die Bezeichnungen im rechtwinkligen Dreieck:
Nach dieser kurzen Wiederholung geht es los. Zum Glück gilt für Dreiecke, dass sie immer ähnlich sind, wenn sie in allen drei Winkeln übereinstimmen. Und genau das brauchen wir jetzt. Nehmen wir uns ein rechtwinkliges Dreieck vor mit γ = 90°. Zugleich legen wir fest: α = 30 °. Zeichnen wir mal ein paar Dreiecke mit diesen Vorgaben aber unterschiedlichen Größen:
Dreieck 1:

Dreieck 2:
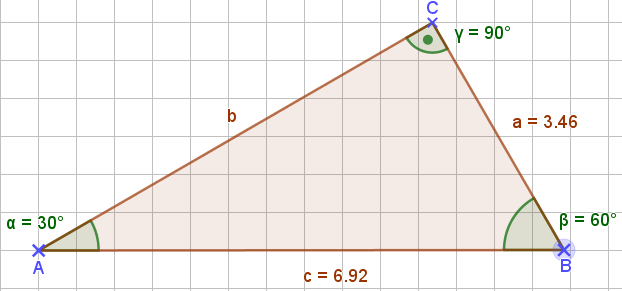
Dreieck 3:
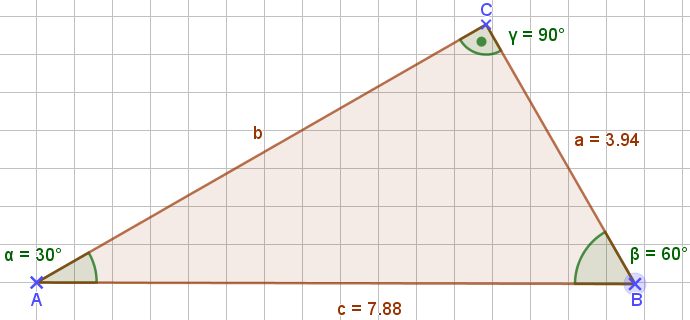
Laut Definition der Ähnlichkeit wissen wir, dass die entsprechenden Seiten der Dreiecke in einem festen Verhältnis zueinanderstehen. Wie sieht es aber innerhalb der Dreiecke aus?
Betrachten wir die Seite a und die Seite c:
Im Dreieck 1 gilt:
\[{{a}\over {c}}~=~{{2,5}\over {5}}~=~0,5\]
Im Dreieck 2:
\[{{a}\over {c}}~=~{{3,46}\over {6,92}}~=~0,5\]
und im Dreieck 3:
\[{{a}\over {c}}~=~{{3,94}\over {7,88}}~=~0,5\]
Wir sehen, im rechtwinkligen Dreieck ist das Verhältnis der Seite, die dem Basiswinkel gegenüberliegt (Gegenkathete) zur Hypotenuse immer gleich. Verändern wir den Wert für α sehen wir, dass sich auch der Wert des Quotienten ändert. Tragen wir die Abhängigkeit von Winkelgröße und Quotient auf, erkennen wir, dass sich das Schaubild einer Funktion ergibt. Und diese Funktion nennen wir Sinusfunktion. Es gilt:
\[\Large sin~\alpha~=~{{a}\over {c}}\]
Natürlich gilt auch:
\[\Large sin~\beta~=~{{b}\over {c}}\]
oder allgemein:
\[\Large sin~x~=~{{Gegenkathete}\over {Hypotenuse}}\]
Zwischen 0° und 360° (Achtung! Standardmäßig werden bei der zeichnerischen Version die Winkel im Bogenmaß verwendet. 0° = 0, 360° = 2 π ≅ 6,28) hat sie folgendes Aussehen:
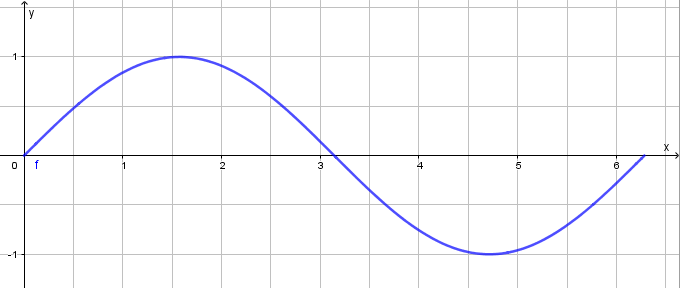
Für Spezialisten: Natürlich hat die Sinusfunktion keine Begrenzung nach links und rechts. Sie ist eine periodische Funktion:

Mit Hilfe der Sinusfunktion können wir im rechtwinkligen Dreieck Strecken und Winkel berechnen. Das war in der Landvermessung eine wichtige Anwendung. Man kann man im Gelände zwar von zwei Stellen aus einen Punkt anvisieren und die Peilwinkel bestimmen, aber häufig ist die Entfernung zwischen den Messtellen nicht immer greifbar, weil Hindernisse im Weg sind (z.B. ein Fluss, Büsche…). Mit Hilfe der Sinusfunktion kann man die Strecke jedoch bequem ausrechnen.
Okay, soweit zum Sinus. Wie sieht das aber mit der anderen Kathete aus? Kommen wir zum
Ganz analog zum Sinus ist auch er der Quotient zweier Seiten, und zwar der Kathete, die dem Winkel anliegt (Ankathete) und der Hypotenuse. Im Fall des Winkels α wäre das dann die Seite b:
\[\Large cos~\alpha~=~{{b}\over {c}}\]
oder
\[\Large cos~x~=~{{Ankathete}\over {Hypotenuse}}\]
Das Schaubild der Funktion ist so ähnlich wie bei der Sinusfunktion, die man 0,5 π in Richtung der x-Achse verschoben hat. Zwischen 0 und 2π hat sie folgendes Aussehen:
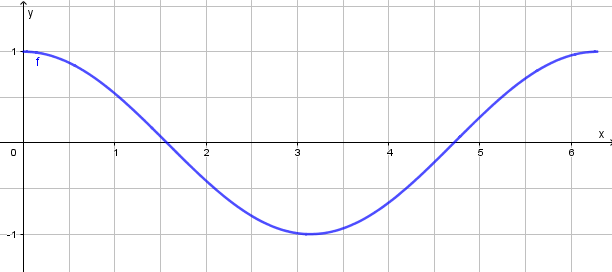
Ansonsten gilt das, was ich auch schon zum Sinus geschrieben habe.
So, dann bliebe noch zu untersuchen, ob bei den Katheten auch etwas Besonderes ist – und wir sind beim
Tatsächlich ergibt auch der Quotient aus Gegenkathete und Ankathete eine Funktion. Diese wird Tangens genannt. Es gilt:
\[\Large tan~\alpha~=~{{a}\over {b}}\]
oder
\[\Large tan~x~=~{{Gegenkathete}\over {Ankathete}}\]
Hier ist das Schaubild zwischen 0 und 2π der Funktion komplett anders.
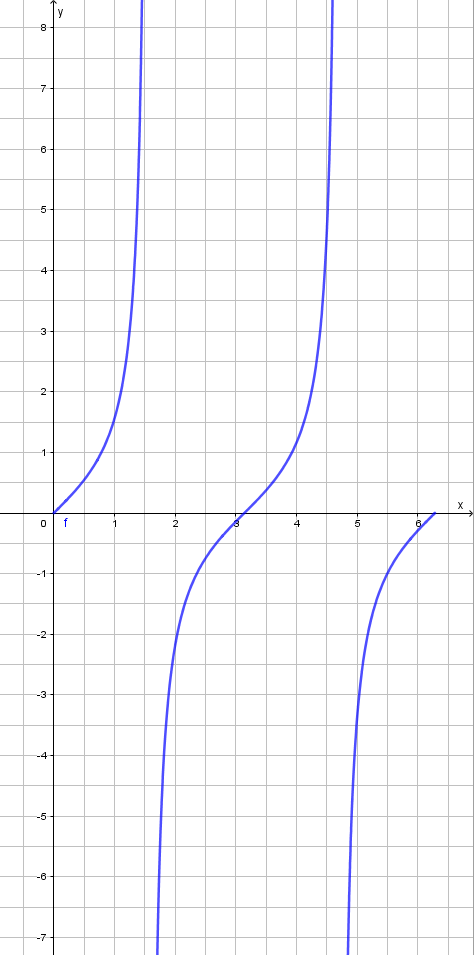
Wir erkennen, dass die Funktion nach oben unbegrenzt verläuft, sich aber an Vielfache von 0,5 π nach oben und unten hin annähert. Das nehmen wir an dieser Stelle mal so hin. Das wird aber denjenigen noch einmal über den Weg laufen, die Mathe in der Sek II betreiben.
Auch zum Tangens existiert das Gegenstück, der
Machen wir es kurz und knapp:
\[\Large cot~\alpha~=~{{b}\over {a}}\]
oder
\[\Large cot~ x~ =~{{Ankathete}\over {Gegenkathete}}\]
So, nun haben wir die vier Winkelfunktionen kennengelernt. Sie ermöglichen uns, in einem rechtwinkligen Dreieck Seitenlängen oder Winkel zu berechnen. Welche man anwendet, hängt natürlich von der Aufgabenstellung ab – oder vom Mathelehrer 😉. Daher: unbedingt eine Planskizze anfertigen! Erkennen wir, dass die Hypotenuse gegeben ist, kommen Sinus oder Cosinus in Frage, wenn nicht, der Tangens. Der Cotangens spielt dabei kaum eine Rolle. Das ist auch okay so, wenn man sich klar macht: habe ich die beiden Katheten gegeben, kann ich immer zu einem Winkel den Tangens aufstellen.
Die Winkelfunktionen sind immer dann hilfreich, wenn ich mit dem Pythagoras nicht weiterkomme. Das ist zum Beispiel so, wenn ich im rechtwinkligen Dreieck nur eine Seite und einen weiteren Winkel (außer dem rechten natürlich 😉) kenne. Von daher sind sie kein Ersatz, sondern eine tolle Ergänzung. Und in den Kapiteln "Sinussatz und Cosinussatz" sehen wir, dass wir auch im „normalen“ Dreieck mit ihnen arbeiten können, was der Pythagoras so nicht schafft.