Zunächst sollten wir uns noch einmal klar machen: Wie zeichne ich einen Winkel möglichst geschickt mit dem Geodreieck? Immer wiede sehe ich, dass die Möglichkeiten des Geodreiecks nicht genutzt werden... Warum einfach, wenn es kompliziert geht? Nein! Ich zeige nochmal auf, wie wir einen Winkel mit dem Geodreieck in einem Rutsch zeichnen können. Dafür wurde das Geodreieck im Übrigen auch konzipiert... Es soll Dinge einfacher machen - und das tut es auch, wenn wir uns darauf einlassen. Also gehen wir noch mal ran. Vor dem Zeichnen eines Winkels im Dreieck müssen wir uns überlegen:
Wozu das Ganze? Nun, wir müssen wissen, auf welcher Skala wir den Winkel ablesen und in welchem Punkt der Scheitelpunkt des Winkels liegt. Damit das klar wird, habe ich auch ein paar Beispiele parat:
Zeichne die Seite c eines Dreiecks mit 7 cm. Trage dann den Winkel α = 75° an.
Okay, gehen wir unsere Punkte durch: α = 75° heißt, es liegt ein spitzer Winkel vor ( < 90°). Der Winkel α hat seinen Scheitelpunkt im PunktA. Dermaßen gestärkt, gehen wir gleich an die Konstruktion:
Zuerst zeichnen wir die Seite c. Damit erhalten wir die PunkteA undB. Wichtig: Die Beschriftung der Punkte machen wir zum Schluss, da wir dann das Geodreieck nicht noch einmal ansetzen müssen (Die Vertreter der reinen Mathelehre mögen mir das bitte verzeihen...). Passenderweise liegt in diesem Beispiel der Nullpunkt des Geodreiecks schon im PunktA.
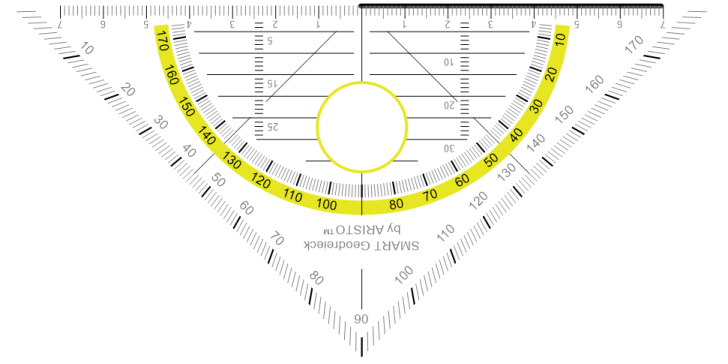
Jetzt müssen wir überlegen, wie der zweite Schenkel des Winkels verläuft. Da es ein spitzer Winkel ist, muss er nach rechts oben verlaufen. Damit brauchen wir dieinnere Skala des Geodreiecks. Wir lassen den Nullpunkt des Geodreiecks im PunktA und drehen das Geodreieck nach links, und zwar solange, bis die 75°-Linie auf der Seite c liegt. Dann müssen wir nur noch vonA aus eine Linie nach oben ziehen und erhalten unseren Winkel α.
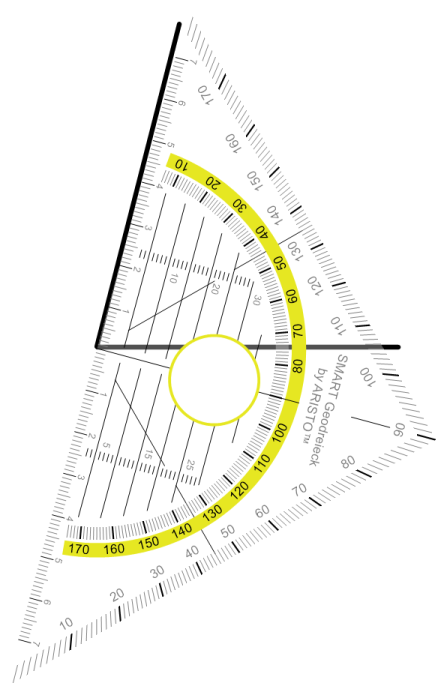
Jetzt noch beschriften und wir sind fertig.

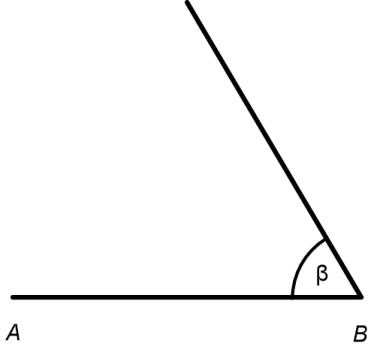
Zeichne die Seite c eines Dreiecks mit 8 cm. Trage dann den Winkel β = 60° an.
Okay, gehen wir unsere Punkte durch: β = 60° heißt, es liegt ein spitzer Winkel vor ( < 90°). Der Winkel β hat seinen Scheitelpunkt im PunktB. Dermaßen gestärkt, gehen wir gleich an die Konstruktion:
Zuerst zeichnen wir die Seite c. Damit erhalten wir die PunkteA undB. Die Beschriftung machen wir wieder zum Schluss. Das Ganze sieht dann so aus:
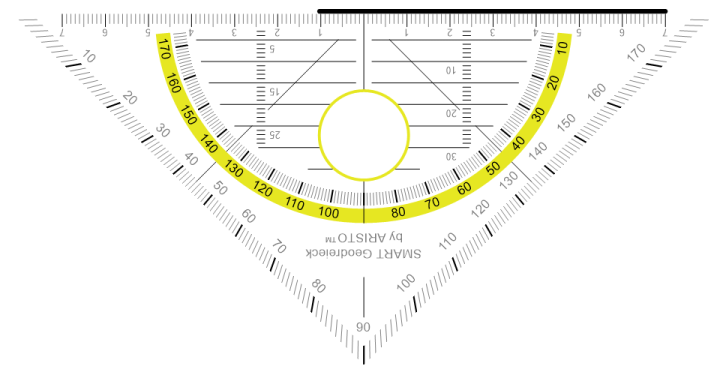
Jetzt müssen wir wieder überlegen, wie der zweite Schenkel des Winkels verläuft. Da es ein spitzer Winkel ist, muss er dieses Mal nach links oben verlaufen. Damit brauchen wir dieäußere Skala des Geodreiecks. Wir legen den Nullpunkt des Geodreiecks auf den PunktB und drehen das Geodreieck nach rechts, und zwar solange, bis die 60°-Linie auf der Seite c liegt. Dann müssen wir nur noch vonB aus eine Linie nach oben ziehen und erhalten unseren Winkel β.
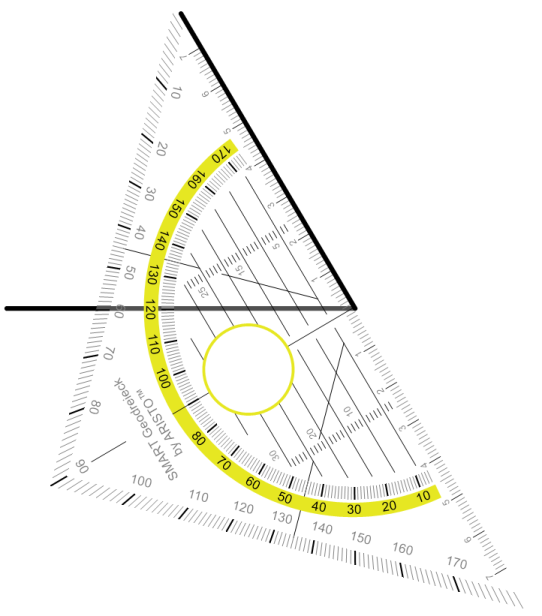
Jetzt noch beschriften und wir sind fertig.
Zeichne die Seite b eines Dreiecks mit 7,5 cm. Trage dann den Winkel γ = 55° an.
Jetzt müssen wir eine kleine Vorüberlegung machen: Gegeben ist die Seite b. Das heißt, ich erhalte die Punkte A undC. Da der PunktC beim Dreieck oben liegt, sollte ich das beim Zeichnen berücksichtigen. Wenn nicht gerade ein stupfwinkliges Dreieck vorliegt, verläuft die Seite b von rechts oben nach links unten. Das sollten wir beim Zeichnen annähernd berücksichtigen; es erleichtert uns das Vorstellungsvermögen deutlich. Okay, gehen wir unsere Punkte durch: γ = 55° heißt, es liegt ein spitzer Winkel vor ( < 90°). Der Winkel γ hat seinen Scheitelpunkt im PunktC. Gehen wir also an die Konstruktion:
Zuerst zeichnen wir die Seite b. Damit erhalten wir die PunkteA undC. Die obere Spitze des Geodreiecks zeigt dabei nach links. Die Beschriftung machen wir wieder zum Schluss. Das Ganze sieht dann so aus:
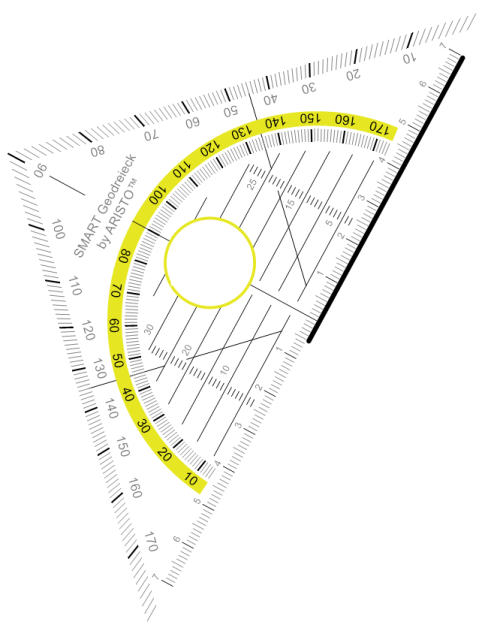
Jetzt müssen wir wieder überlegen, wie der zweite Schenkel des Winkels verläuft. Da es ein spitzer Winkel ist, muss er nach rechts unten verlaufen. Damit brauchen wir dieinnere Skala des Geodreiecks. Wir legen den Nullpunkt des Geodreiecks auf den PunktC und drehen das Geodreieck nach links, und zwar solange, bis die 55°-Linie auf der Seite b liegt. Dann müssen wir nur noch vonC aus eine Linie nach unten ziehen und erhalten unseren Winkel γ.
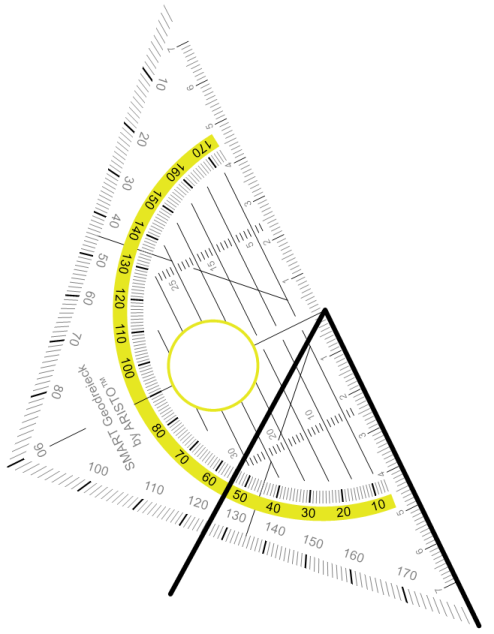
Jetzt noch beschriften und wir sind fertig.
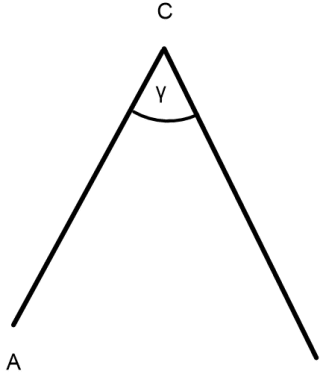
Zeichne die Seite c eines Dreiecks mit 9 cm. Trage dann den Winkel α = 110° an.
Okay, gehen wir unsere Punkte durch: α = 110° heißt, es liegt ein stumpfer Winkel vor ( > 90°). Der Winkel α hat seinen Scheitelpunkt im PunktA. Danmit gehen wir an die Konstruktion:
Zuerst zeichnen wir die Seite c. Damit erhalten wir die PunkteA undB.
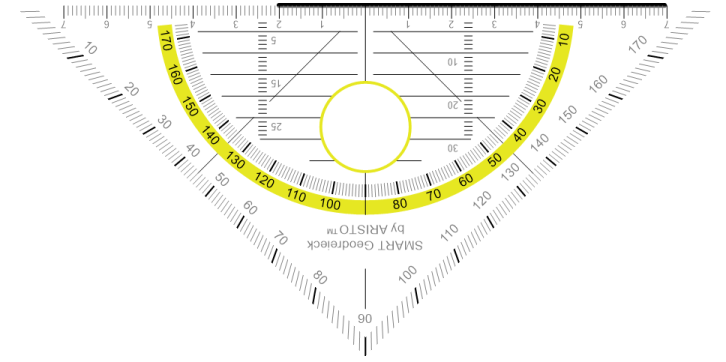
Jetzt müssen wir wieder überlegen, wie der zweite Schenkel des Winkels verläuft. Da es ein stumpfer Winkel ist, muss er nach links oben verlaufen. Damit brauchen wir dieinnere Skala des Geodreiecks. Wir schieben den Nullpunkt des Geodreiecks auf den PunktA und drehen das Geodreieck nach links, und zwar solange, bis die 110°-Linie auf der Seite c liegt. Dann müssen wir nur noch vonA aus eine Linie nach links oben ziehen und erhalten unseren Winkel α.
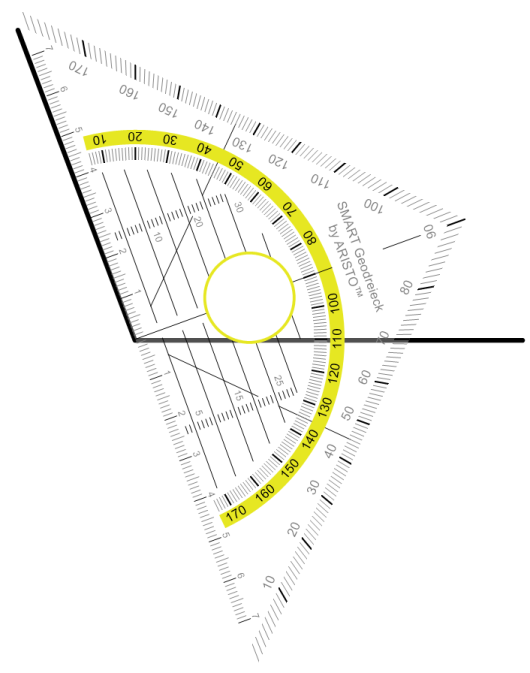
Jetzt noch beschriften und wir sind fertig.
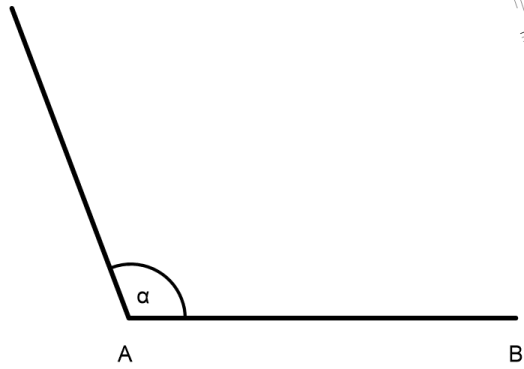
So, dies waren ein paar Beispiele, wie wir in Dreiecken Winkel zeichnen können. Ich hoffe, nach diesem Kapitel sollten das kein Problem mehr darstellen. Damit sind wir nun bestens gerüstet, Dreiecke zu konstruieren. Das machen wir im Kapitel "Kongruenz bei Dreiecken".
Zum Schluss noch ein kleiner Tipp: Beim Zeichnen der Seiten und Winkel das Geodreieck immer so legen, dass die obere Spitze des Geodreiecks aus dem zu zeichnenden Dreieck herausragt, so wie ich das in meinen Beispielen immer gemacht habe. Dann haben wir weniger Probleme zu überlegen, wie ich das Dreieck zum Zeichnen der Winkel drehen muss und bekommen keinen Knoten in der Hand. 😉