Die Multiplikation von Vektoren ist leider nicht so einfach und eindeutig, wie bei den „normalen“ Zahlen. Wir müssen hier drei Fälle unterscheiden. Ich versuche mein Möglichstes, dass uns das so einsichtig wie möglich wird. Ich verzichte bewusst auf aufwändige Herleitungen und möchte euch eine Hilfe zum Umgang mit den drei Arten geben. Das wird für die meisten von euch auch völlig hinreichen, die einfach nur „überleben“ möchten. Dennoch kommen wir nicht ganz um die Bedeutung der drei Verfahren herum. Ein paar wenige Standardbeispiele zum Umgang damit werde ich euch auch bieten. Das erhebt keinen Anspruch auf Vollständigkeit, soll aber ein Gefühl für das Ganze vermitteln.
Okay, kommen wir zum ersten Teil, der
Das ist der einfachste der drei Fälle. Bei der Multiplikation eines Vektors mit einer positiven (reellen) Zahl, wird nur der Betrag (die Länge) des Vektors geändert. Beispiel:
Gegeben ist der Vektor
\[\vec{u} = \begin{pmatrix} 3 \\4 \end{pmatrix}\]
gesucht ist:
\[\vec{w} = 2~ \vec{u}\]
Die Multiplikation wird durchgeführt, indem alle einzelnen Komponenten des Vektors \(\vec{v}\) mit 2 multipliziert werden:
\[\vec{w} = a~ \vec{u} = \begin{pmatrix} {a \cdot u_x} \\{a \cdot u_y} \end{pmatrix}\]
Geometrisch sieht das so aus (\(\vec{v}\) grün):
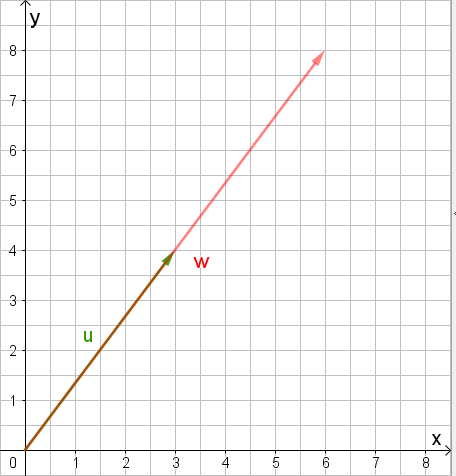
Und rechnerisch sieht das so aus:
\[\vec{w} = 2~ \cdot \begin{pmatrix} 3 \\4 \end{pmatrix} = \begin{pmatrix} {2 \cdot 3} \\{2 \cdot 4} \end{pmatrix} = \begin{pmatrix} 6 \\8 \end{pmatrix}\]Manche Mathelehrer mögen an dieser Stelle noch zwei Begriffe: Liegt a zwischen 0 und 1, wird der Ausgangsvektor gestaucht, ist a größer als 1 wird der Vektor gestreckt.
Was passiert aber, wenn a negativ ist? Dann wir zusätzlich noch die Richtung des Vektors umgekehrt. In der folgenden Abbildung wird das gezeigt an
\[\vec{w} = -~2~ \vec{u}\]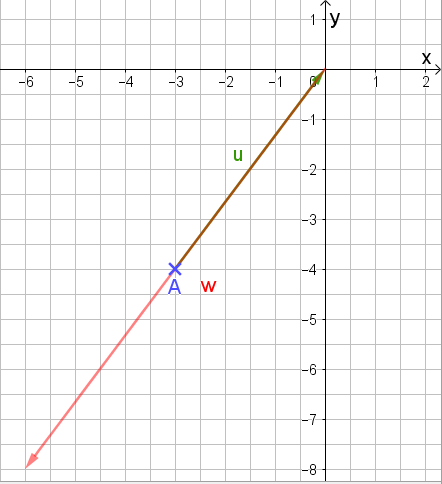
Das Ganze gilt natürlich auch für den dreidimensionalen Raum. In der Spaltenschreibweise muss dann noch unten \(u_z\) ergänzt werden. Damit wäre dieser Teil abgeschlossen und wir kommen zum
Beim Skalarprodukt werden zwei Vektoren miteinander multipliziert. Es ist festgelegt als das Produkt der Beträge der beiden Vektoren mit dem Cosinus des eingeschlossenen Winkels. Das Ergebnis ist eine Zahl (auch: Skalar). Hört sich kompliziert an? Wirklich???? Dann solltet ihr euch diesen Satz (entnommen dem Wikipedia-Artikel über das Skalarprodukt, Stand 01.04.2021) anschauen:„Ein Skalarprodukt ist … eine Funktion, die zwei Elementen eines reellen oder komplexen Vektorraums einen Skalar zuordnet, genauer eine (positiv definite) hermitesche Sesquilinearform, bzw. spezieller bei reellen Vektorräumen eine (positiv definite) symmetrische Bilinearform.“ Ich denke, unsere Definition ist da etwas harmloser… 😉 Gut, machen wir uns das Ganze an einem kleinen Beispiel deutlich:
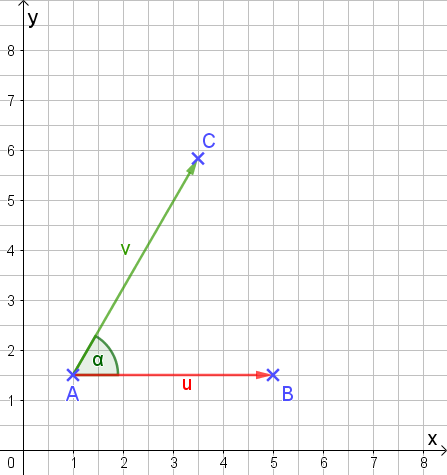
Wir sehen die beiden Vektoren (\(\vec{u}\) rot und \(\vec{v}\) grün) und den Winkel, den die beiden miteinander bilden. Wie wir den Betrag eines Vektors berechnen, haben wir schon kennengelernt. Wir könnten jetzt also die Beträge der beiden Vektoren ausrechnen, sie addieren und dann mit dem Cosinus des Winkels (hier 60°) multiplizieren. Zum Glück geht es Dank der Komponentenschreibweise deutlich einfacher! 😊 Wir berechnen zeilenweise das Produkt der Komponenten und addieren zum Schluss alles. Allgemein sieht das so aus:
\[\vec{u} \cdot \vec{v} = u_x \cdot v_x + u_y \cdot v_y\]bzw.
\[\vec{u} \cdot \vec{v} = u_x \cdot v_x + u_y \cdot v_y + u_z \cdot v_z\]Achtung! Hier gibt es noch andere Schreibweisen, nämlich:
\[\vec{u} \bullet \vec{v}~oder~ \vec{u} \circ \vec{v}\]Hier bitte aufpassen, welches Hobby euer Mathelehrer hat 😉!
Nach so viel Formelkram werden wir konkreter. Bilde das Skalarprodukt der Vektoren
Das war’s, alles völlig unspektakulär… 😉
Aaaber… Da gibt es noch zwei Sonderfälle, die ich auf jeden Fall betrachten möchte. Kommen wir zum ersten:
Huch! Was ist passiert? Warum ist das so?
Wir haben ja festgelegt haben, dass das Skalarprodukt das Produkt der Beträge der beiden Vektoren mit dem Cosinus des eingeschlossenen Winkels ist, also:
Die Beträge der drei Vektoren sind ja nicht null. Ein Produkt kann nur null werden, wenn einer der Faktoren null wird – und das geht hier nur, wenn cos (α) gleich null ist – und das ist bei 90° der Fall – denn cos(90°) = 0. Damit müssen die beiden Vektoren senkrecht aufeinander stehen. Das Skalarprodukt können wir also dazu verwenden, um zu überprüfen, ob zwei Vektoren senkrecht aufeinander stehen. Dann ist es nämlich 0.
Wir können natürlich auch einen zweiten Vektor bestimmen, der auf dem ersten senkrecht steht. Dazu brauchen wir aber vom 2. Vektor zwei (bzw. eine Komponente in 2D) vorgegebene Komponenten. Ein Beispiel: Wie muss ein Vektor \(\vec{v}\) verlaufen, damit er auf \(\vec{u}\) senkrecht steht?
\[\vec{u} = \begin{pmatrix} 2 \\1 \\2 \end{pmatrix} ~und~ \vec{v} = \begin{pmatrix} x \\4 \\-5 \end{pmatrix}\] \[\vec{u} \cdot \vec{v} = 2 \cdot x + 1 \cdot 4 + 2 \cdot (-5)\]Damit die beiden Vektoren senkrecht aufeinander stehen, muss der Term
\[2 \cdot x + 1 \cdot 4 + 2 \cdot (-5)\]gleich 0 werden, also:
\begin{align} 2 \cdot x + 1 \cdot 4 + 2 \cdot (-5) &= 0\\ 2 \cdot x + 4 - 10 &= 0\\ 2 \cdot x &= 6\\ x &= 3 \end{align}
Damit lautet \(\vec{v}\) nun vollständig:
\[\vec{v} = \begin{pmatrix} 3 \\4 \\-5 \end{pmatrix}\]Damit haben wir den ersten der beiden Fälle abgeschlossen, die ich noch behandeln wollte. Kommen wir zum zweiten Fall und schauen uns folgendes Skalarprodukt an:
\[\vec{u} = \begin{pmatrix} 3 \\4 \end{pmatrix} ~und~ \vec{v} = \begin{pmatrix} 6 \\8 \end{pmatrix}\] \[\vec{u} \cdot \vec{v} = 3 \cdot 6 + 4 \cdot 8 = 50\]Hmmm…. Was ist da so besonders dran? Ist doch alles ganz normal - oder???? Okay, schauen wir uns mal die Beträge der beiden Vektoren an:
\[\vert\vec{u}\vert = \sqrt{9 + 16} = 5\] \[\vert\vec{v}\vert = \sqrt{36 + 64} = 10\]wegen
\[\vec{u} \cdot \vec{v} = \vert\vec{u}\vert \cdot \vert\vec{v}\vert \cdot cos(\alpha)\]muss hier gelten: cos(α) = 1 (Ergebnis: 50). Da gilt: cos(0°) = 1 heißt das, die beiden Vektoren bilden keinen Winkel miteinander, sie sind parallel! Damit haben wir ein prima Mittel in die Hand bekommen, zwei Vektoren auf Parallelität zu testen. Sind sie parallel gilt nämlich:
\[\vec{u} \cdot \vec{v} = \vert\vec{u}\vert \cdot \vert\vec{v}\vert \]Wir können auch sonst noch ein paar Dinge mit dem Skalarprodukt anfangen, aber ich denke, das sind die wichtigsten. Und wenn ihr jetzt fragt, wo braucht man das, so gebe ich euch zumindest ein Beispiel aus der Physik. Die Arbeit entlang eines Weges ist nämlich definiert als
\[w = \vec{F} \cdot \vec{s} \]Die Arbeit ist also nichts anderes als das Skalarprodukt aus Kraft und Strecke.
Aller guten Dinge sind drei. Hier kommt die letzte Methode, zwei Vektoren miteinander zu multiplizieren, nämlich das
Während die ersten Methoden sowohl in der Ebene als auch im Raum funktionieren, geht es beim Kreuzprodukt grundsätzlich nur im Raum. Warum, werden wir gleich sehen. Das Kreuzprodukt zweier Vektoren ist nämlich ein dritter Vektor, der auf beiden Ursprungsvektoren senkrecht steht. Das geht aber nur, wenn der dann in den Raum zeigt. Der Betrag des neuen Vektors ist genauso groß wie die Fläche des Parallelogramms, das die beiden Ursprungsvektoren aufspannen.
Okay, machen wir das scheibchenweise… Schauen wir uns zunächst zwei Ursprungsvektoren an:
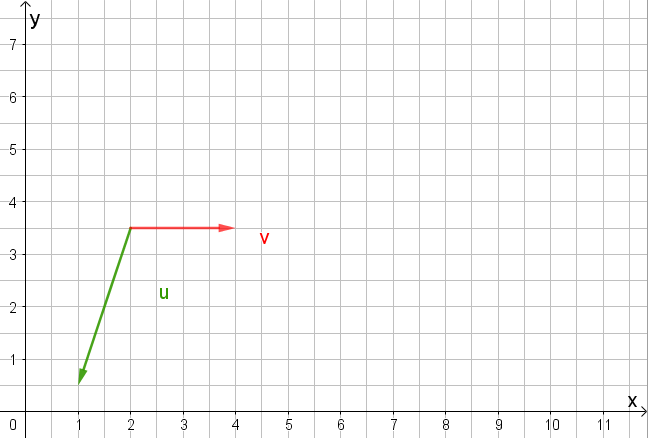
Das sind die zwei Vektoren in der x-y-Ebene. Die können wir zu einem Parallelogramm ergänzen:
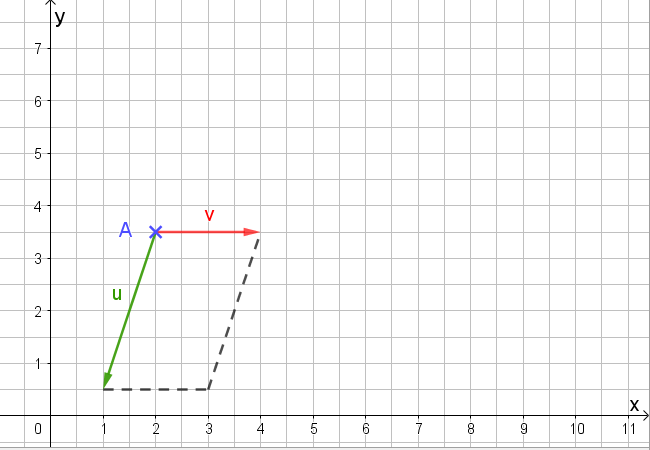
Die Fläche des Parallelogramms berechnet sich nach
\[A = \vert\vec{v}\vert \cdot h = 2 \cdot 3 = 6\]Schauen wir, was herauskommt, wenn ich das Kreuzprodukt zwischen beiden Vektoren bilde. Es ergibt sich ein Vektor, der senkrecht auf beiden Ursprungsvektoren steht, nämlich
\[\vec{u} = \begin{pmatrix} 0 \\0 \\6 \end{pmatrix}\]Wie wir zum Ergebnis kommen, zeige ich weiter unten. Dieser Vektor hat den Betrag:
\[\vert\vec{w}\vert = \sqrt{w_x^2 + w_y^2 + w_z^2} = \sqrt{0 + 0 + 6^2} = 6\]Das ist aber genau der Wert, den wir eben für die Fläche des Parallelogramms ausgerechnet haben, das die beiden Ausgangsvektoren aufspannen. Super, das passt! 😊
So, das war jetzt erst mal die einfache Veranschaulichung. Wie wir das Kreuzprodukt berechnen, folgt jetzt. Die Herleitung ist nicht ganz so einfach, daher begnügen wir uns mit dem Endergebnis 😉. Als Multiplikationszeichen dient beim Kreuzprodukt ein „x“. Die Berechnung erfolgt nach der folgenden Formel:
\[\vec{w} = \vec{u} \times \vec{v} = \begin{pmatrix} {u_y \cdot v_z - u_z \cdot v_y} \\{u_z \cdot v_x - u_x \cdot v_z} \\{u_x \cdot v_y - u_y \cdot\ v_x} \end{pmatrix}\]Sieht kompliziert aus? Okay, nehmen wir uns hier zwei weitere Beispiele vor. Zunächst nehmen wir die Ursprungsvektoren aus unserem Beispiel:
\[\vec{w} = \vec{u} \times \vec{v} = \begin{pmatrix} -1 \\-3 \\0 \end{pmatrix} \times \begin{pmatrix} 2 \\ 0 \\0 \end{pmatrix}\] \[\vec{w} = \begin{pmatrix} {-3 \cdot 0 - 0 \cdot 0} \\{0 \cdot 2 - (-1) \cdot 0} \\{-1 \cdot 0 - (-3) \cdot 2} \end{pmatrix} = \begin{pmatrix} 0 \\0 \\6 \end{pmatrix}\]Super, passt! 😊
Zeichnerisch sieht das ganze dann so aus: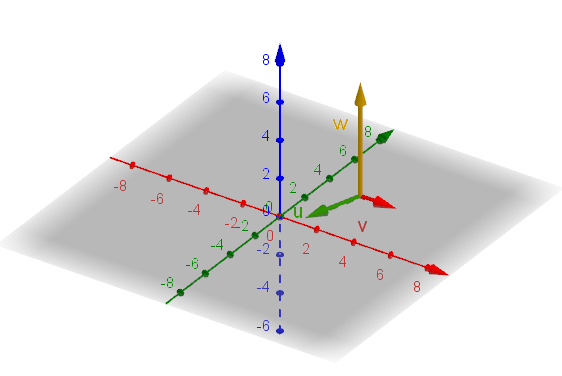
Nun folgt ein zweites Beispiel, mit zwei Vektoren, die beliebig im Raum liegen:
\[\vec{w} = \vec{u} \times \vec{v} = \begin{pmatrix} 1 \\4 \\3 \end{pmatrix} \times \begin{pmatrix} 2 \\ 5 \\6 \end{pmatrix}\] \[\vec{w} = \begin{pmatrix} {4 \cdot 6 - 3 \cdot 5} \\{3 \cdot 2 - 1 \cdot 6} \\{1 \cdot 5 - 4 \cdot 2} \end{pmatrix} = \begin{pmatrix} 9 \\0 \\-3 \end{pmatrix}\]Auch das ist hier noch einmal bildlich dargestellt:
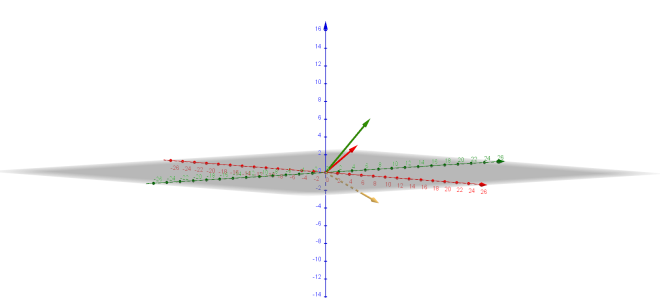
Wenn man die Formel daneben liegen hat, ist das zwar ungewohnt, aber gar nicht so schwer… Und nun die Frage: Braucht man das? Aber ja. In der Physik gibt es ja den berühmten Schaukelleiter-Versuch. Mit der 3-Finger-Regel kann man dann herausfinden, in welche Richtung der Leiter aus dem Magnetfeld gedrückt wird. Das ist im Prinzip (vereinfacht!) nichts anderes als das Kreuzprodukt aus Stromrichtung und Richtung des Magnetfeldes. Für Spezialisten: Das Ergebnis trägt den Namen Lorentzkraft. Das ist nicht die einzige Stelle, wo uns das über den Weg läuft, auch beim Drehmoment und vielen anderen Größen kommt das immer wieder vor.