Bevor wir mit Geraden weiterarbeiten, brauchen wir noch eine Definition vorweg:
Das lässt sich trotz des sperrigen Namens recht gut beschreiben.
Zwei Vektoren sind kollinear, wenn ein Vektor ein Vielfaches des anderen ist.
Nehmen wir die Vektoren
\[\vec{u} = \begin{pmatrix} 1 \\1 \\3 \end{pmatrix} ~und~ \vec{v} = \begin{pmatrix} -2 \\-2 \\-6 \end{pmatrix}\]
Jetzt muss ich untersuchen, ob es ein λ gibt, so das gilt:
\[\vec{v} = \lambda~ \cdot~ \vec{u}\]
Ich erhalte:
\[\begin{pmatrix} -2 \\-2 \\-6 \end{pmatrix} = \lambda~ \cdot \begin{pmatrix} 1 \\1 \\3 \end{pmatrix}\]
Wir lösen zeilenweise auf und erhalten
\begin{align} – 2 &= λ\\ – 2 &= λ\\ – 6 &= 3 λ\\ \end{align}
Wir erhalten also für alle drei Komponenten: λ = – 2. Damit sind die beiden Vektoren kollinear. Wenn auch bei nur einer der drei Komponenten ein anderes λ herauskommt, sind sie nicht kollinear.
Nehmen wir die Gerade
\[g: ~ \vec{x} = \begin{pmatrix} 1 \\4 \\3 \end{pmatrix} + \lambda \begin{pmatrix} 1 \\1 \\3 \end{pmatrix}\]
und den Punkt P (4 | 7 | 12). Wir setzen die Koordinaten des Punktes für \(\vec{x}\) ein:
\[\begin{pmatrix} 4 \\7 \\12 \end{pmatrix}= \begin{pmatrix} 1 \\4 \\3 \end{pmatrix} + \lambda \begin{pmatrix} 1 \\1 \\3 \end{pmatrix}\]
Wir formen um:
\begin{align} \begin{pmatrix} 4 \\7 \\12 \end{pmatrix} - \begin{pmatrix} 1 \\4 \\3 \end{pmatrix} &= \lambda \begin{pmatrix} 1 \\1 \\3 \end{pmatrix}\\ \\ \begin{pmatrix} 4 - 1 \\7 - 4 \\12 - 3 \end{pmatrix} &= \lambda \begin{pmatrix} 1 \\1 \\3 \end{pmatrix}\\ \\ \begin{pmatrix} 3 \\3 \\9 \end{pmatrix} &= \begin{pmatrix} \lambda \\\lambda \\3~ \lambda \end{pmatrix}\\ \end{align}
Nun müssen wir zeilenweise nach λ auflösen.
\begin{align} 3 &= λ\\ 3 &= λ\\ 9 &= 3~ λ\\ \end{align}
Wir erhalten in jeder Zeile: λ = 3. Damit liegt der Punkt P auf der Geraden.
Bitte aufpassen: wir müssen wirklichalle Komponenten untersuchen. Nur wenn wir für alle drei Komponenten denselben Wert für λ erhalten, liegt der Punkt auf der Geraden.
In der Ebene haben wir da keine Probleme. Wenn die Geraden nicht gerade parallel sind, schneiden sie sich immer. Aber wir arbeiten hier im Raum. Hier gilt es, mehrere Fälle zu unterscheiden:
Zum Glück können wir die Fälle 1 und 2 zusammenfassen, ebenso die Fälle drei und vier. Also beantworten wir zuerst die Frage
Das entscheidende sind die beiden Richtungsvektoren. Sind sie kollinear (s.o.), sind die Geraden parallel oder identisch. Des Weiteren muss ich prüfen, ob ein Punkt auf der einen Gerade auch auf der anderen Gerade liegt. Wenn ja, sind die Geraden identisch, wenn nein, sind sie parallel. Um die Sache hier einfacher zu machen, nehmen wir den Stützpunkt der jeweiligen Geraden. Den können wir ja direkt ablesen. Nehmen wir uns gleich ein konkretes Beispiel vor. Gegeben sind die beiden Geraden
\[g: ~ \vec{x} = \begin{pmatrix} 1 \\4 \\3 \end{pmatrix} + \lambda \begin{pmatrix} 1 \\1 \\3 \end{pmatrix}\ und~ h: ~ \vec{x} = \begin{pmatrix} -1 \\4 \\-3 \end{pmatrix} + \mu \begin{pmatrix} -2 \\-2 \\6 \end{pmatrix}\]
Überprüfen wir zuerst, ob die beiden Richtungsvektoren kollinear sind (s.o.):
\[\begin{pmatrix} -2 \\-2 \\-6 \end{pmatrix} = \nu \begin{pmatrix} 1 \\1 \\3 \end{pmatrix}\]
Wir lösen Zeile für Zeile auf:
\begin{align} – 2 &= ν\\ – 2 &= ν\\ – 6 &= 3~ ν \end{align}
Wir erhalten also für alle drei Komponenten: ν = – 2. Damit sind die beiden Richtungsvektoren kollinear. Das heißt, die beiden Geraden sind also entweder identisch oder wirklich parallel. Um das zu überprüfen, setze ich den Stützvektor von h in g ein:
\[\begin{pmatrix} -1 \\4 \\-3 \end{pmatrix} = \begin{pmatrix} 1 \\4 \\3 \end{pmatrix} + \lambda \begin{pmatrix} 1 \\1 \\3 \end{pmatrix}\]
und erhalte
\begin{align} \begin{pmatrix} -1 \\4 \\-3 \end{pmatrix} - \begin{pmatrix} 1 \\4 \\3 \end{pmatrix} &= \lambda \begin{pmatrix} 1 \\1 \\3 \end{pmatrix}\\ \\ \begin{pmatrix} -1 - 1\\4 - 4 \\-3 - 3 \end{pmatrix} &= \lambda \begin{pmatrix} 1 \\1 \\3 \end{pmatrix}\\ \\ \begin{pmatrix} -2 \\0 \\-6 \end{pmatrix} &= \lambda \begin{pmatrix} 1 \\1 \\3 \end{pmatrix}\\ \end{align}
und damit die drei Gleichungen:
\begin{align} – 2 &= λ\\ 0 &= λ\\ – 6 &= 3 λ\\ \end{align}
Für die erste und dritte Zeile erhalte ich λ = – 2, aber nicht für die zweite Zeile. Damit liegt der Stützpunkt von h nicht auf g. Daher sind beide Geraden wirklich parallel. Wenn wir für alle drei Zeilen das gleiche Ergebnis erhielten, wären die beiden Geraden identisch.
Das ist doch gar nicht sooo schwer 😉
Bevor wir uns mit den anderen beiden Fällen beschäftigen, brauchen wir noch eine Definition:
Zwei Geraden, die weder parallel noch identisch sind und sich nicht schneiden, nennen wir windschiefe Geraden.
Auch das ist jetzt nicht wirklich schwer, das hat man so festgelegt und so benannt. Okay, kommen wir also zu der Frage
Hier gehen wir in folgender Reihenfolge vor:
Auch hier nehmen wir uns lieber ein Beispiel vor, bevor es zu abstrakt wird.
Gegeben sind die Geraden
\[g: ~ \vec{x} = \begin{pmatrix} 1 \\4 \\3 \end{pmatrix} + \lambda \begin{pmatrix} 1 \\1 \\3 \end{pmatrix}\ und~ h: ~ \vec{x} = \begin{pmatrix} -1 \\4 \\-3 \end{pmatrix} + \mu \begin{pmatrix} 2 \\4 \\-6 \end{pmatrix}\]
Schritt 1: Wir überprüfen zuerst, ob die beiden Richtungsvektoren kollinear sind:
\begin{align} \begin{pmatrix} 2 \\4 \\-6 \end{pmatrix} &= \nu~ \begin{pmatrix} 1 \\1 \\3 \end{pmatrix}\\ \\ 2 &= ν\\ 4 &= ν\\ – 6 &= 3~ ν\\ \end{align}
Da wir für ν drei verschiedene Werte erhalten, sind die beiden Richtungsvektoren nicht kollinear. Daher schneiden sich die Geraden entweder in einem Punkt oder sie sind windschief.
Schritt 2: Wir setzen beide Geradengleichungen gleich:
\[\begin{pmatrix} 1 \\4 \\3 \end{pmatrix} + \lambda \begin{pmatrix} 1 \\1 \\3 \end{pmatrix} = \begin{pmatrix} -1 \\4 \\-3 \end{pmatrix} + \mu \begin{pmatrix} 2 \\4 \\-6 \end{pmatrix}\]
Schritt 3: Wir formen um und erhalten drei Gleichungen mit zwei Unbekannten:
\begin{align} \begin{pmatrix} 1 \\4 \\3 \end{pmatrix} - \begin{pmatrix} -1 \\4 \\-3 \end{pmatrix} &= - \lambda \begin{pmatrix} 1 \\1 \\3 \end{pmatrix} + \mu \begin{pmatrix} 2 \\4 \\-6 \end{pmatrix}\\ \\ \begin{pmatrix} 1 - (-1) \\4 - 4 \\3 - (-3) \end{pmatrix} &= - \lambda \begin{pmatrix} 1 \\1 \\3 \end{pmatrix} + \mu \begin{pmatrix} 2 \\4 \\-6 \end{pmatrix}\\ \\ \begin{pmatrix} 2 \\0 \\6 \end{pmatrix} &= - \lambda \begin{pmatrix} 1 \\1 \\3 \end{pmatrix} + \mu \begin{pmatrix} 2 \\4 \\-6 \end{pmatrix}\\ \\ a)~~ 2~ &=~ – λ + 2~μ\\ b)~~ 0~ &=~ – λ + 4~μ\\ c)~~ 6~ &=~ – 3~λ~–~ 6~μ\\ \end{align}
Schritt 4: Wir lösen das Gleichungssystem:
Nehmen wir die Gleichungen a) und b):
\begin{align} a)~~ 2 &=~ –~ λ~ + 2~ μ~~~ |~ ·~ ( – 1) \\ b)~~ 0 &=~ –~ λ~ + 4~ μ\\ \\ – 2 &=~ λ~ –~ 2~ μ\\ 0 &=~ – λ~ + 4~ μ\\ \end{align}
Wir addieren und setzen das Ergebnis für μ in a) ein:
\begin{align} – 2 &= 2~ μ ~~~|~ :~ 2\\ – 1 &= μ\\ \\ a)~~ 2 &=~ – λ + 2~ (– 1)\\ 2 &=~ – λ~ – 2 ~~~|~ + 2\\ 4 &=~ – λ ~~~|~ · ( – 1)\\ – 4 &= λ\\ \end{align}
Schritt 5: Wir setzen die gefundene Lösungen in die bislang nicht benutzte Gleichung c) ein:
\begin{align} c)~~ 6 &=~ – 3~ λ~ –~ 6~ μ\\ 6 &=~ – 3~ (– 4)~ –~ 6~ ( – 1)\\ 6 &= 12 + 6 \\ 6 &= 18 \\ \end{align}
Schritt 6: Wir werten das Ergebnis aus Schritt 5:
Wir sehen, es ergibt sich eine unwahre Aussage (6 = 18). Das bedeutet, die beiden Geraden schneiden sich nicht, sondern sind windschief.
Super! Das ist zwar zum Teil etwas aufwändig, aber nicht schwer. Schließlich benutzen wir nur Kenntnisse aus der S I. Ich weiß, es gibt hier die Möglichkeit mit Determinanten zu arbeiten. Aber ob das wirklich immer einfacher und schneller ist, mit einer 3 x 3 Determinante zu arbeiten, weiß ich nicht. Ich bin in der Regel schneller mit obigem Weg. Aber: jeder wie er mag. Ich wollte die Möglichkeit wenigstens erwähnen, aber nicht vertiefen.
Schauen wir uns noch an, was passiert, wenn die Geraden sich schneiden:
Gegeben sind die Geraden
\[g: ~ \vec{x} = \begin{pmatrix} 1 \\4 \\3 \end{pmatrix} + \lambda \begin{pmatrix} 1 \\1 \\3 \end{pmatrix}\ und~ h: ~ \vec{x} = \begin{pmatrix} -1 \\4 \\-3 \end{pmatrix} + \mu \begin{pmatrix} 2 \\4 \\6 \end{pmatrix}\]
Schritt 1: Wir überprüfen zuerst, ob die beiden Richtungsvektoren kollinear sind:
\begin{align} \begin{pmatrix} 2 \\4 \\6 \end{pmatrix} &= \nu~ \begin{pmatrix} 1 \\1 \\3 \end{pmatrix}\\ \\ 2 &= ν\\ 4 &= ν\\ 6 &= 3~ ν\\ \end{align}
Da wir für ν zwei verschiedene Werte erhalten, sind die beiden Richtungsvektoren nicht kollinear. Daher schneiden sich die Geraden entweder in einem Punkt oder sie sind windschief.
Schritt 2: Wir setzen beide Geradengleichungen gleich:
\[\begin{pmatrix} 1 \\4 \\3 \end{pmatrix} + \lambda \begin{pmatrix} 1 \\1 \\3 \end{pmatrix} = \begin{pmatrix} -1 \\4 \\-3 \end{pmatrix} + \mu \begin{pmatrix} 2 \\4 \\6 \end{pmatrix}\]
Schritt 3: Wir formen um und erhalten drei Gleichungen mit zwei Unbekannten:
\begin{align} \begin{pmatrix} 1 \\4 \\3 \end{pmatrix} - \begin{pmatrix} -1 \\4 \\-3 \end{pmatrix} &= - \lambda \begin{pmatrix} 1 \\1 \\3 \end{pmatrix} + \mu \begin{pmatrix} 2 \\4 \\6 \end{pmatrix}\\ \\ \begin{pmatrix} 1 - (-1) \\4 - 4 \\3 - (-3) \end{pmatrix} &= - \lambda \begin{pmatrix} 1 \\1 \\3 \end{pmatrix} + \mu \begin{pmatrix} 2 \\4 \\6 \end{pmatrix}\\ \\ \begin{pmatrix} 2 \\0 \\6 \end{pmatrix} &= - \lambda \begin{pmatrix} 1 \\1 \\3 \end{pmatrix} + \mu \begin{pmatrix} 2 \\4 \\6 \end{pmatrix}\\ \\ a)~~ 2 &=~ – λ + 2~μ\\ b)~~ 0 &=~ – λ + 4~μ\\ c)~~ 6 &=~ – 3~λ~+ 6~μ\\ \end{align}
Schritt 4: Wir lösen das Gleichungssystem:
Nehmen wir die Gleichungen a) und b):
\begin{align} a)~~ 2 &=~ –~ λ~ + 2~ μ~~~ |~ ·~ ( – 1) \\ b)~~ 0 &=~ –~ λ~ + 4~ μ\\ \\ – 2 &=~ λ~ –~ 2~ μ\\ 0 &=~ – λ~ + 4~ μ\\ \end{align}
Wir addieren und setzen das Ergebnis für μ in a) ein:
\begin{align} – 2 &= 2~ μ ~~~|~ :~ 2\\ – 1 &= μ\\ \\ a)~~ 2 &=~ – λ + 2~ (– 1)\\ 2 &=~ – λ~ – 2 ~~~|~ + 2\\ 4 &=~ – λ ~~~|~ · ( – 1)\\ – 4 &= λ\\ \end{align}
Schritt 5: Wir setzen die gefundene Lösungen in die bislang nicht benutzte Gleichung c) ein:
\begin{align} c)~~ 6 &=~ – 3~ λ~ +~ 6~ μ\\ 6 &=~ – 3~ (– 4)~ +~ 6~ ( – 1)\\ 6 &= 12 - 6 \\ 6 &= 6 \\ \end{align}
Schritt 6: Wir werten das Ergebnis aus Schritt 5:
Wir sehen, es ergibt sich eine wahre Aussage (6 = 6). Das bedeutet, die beiden Geraden schneiden sich in einem Punkt. Diesen Schnittpunkt können wir jetzt ausrechnen. Wir setzen die erhaltenen Werte für λ bzw. μ in die jeweilige Geradengleichung ein. Dann rechnen wir aus und erhalten den Schnittpunkt. Probieren wir das mit dem Wert für λ:
\begin{align} g: ~ \vec{x} &= \begin{pmatrix} 1 \\4 \\3 \end{pmatrix} + (-~4) \cdot \begin{pmatrix} 1 \\1 \\3 \end{pmatrix}\\ \\ \vec{x} &= \begin{pmatrix} 1 \\4 \\3 \end{pmatrix} + \begin{pmatrix} -4 \\-4 \\-12 \end{pmatrix}\\ \\ \vec{x} &= \begin{pmatrix} -3 \\0 \\-9 \end{pmatrix}\\ \end{align}
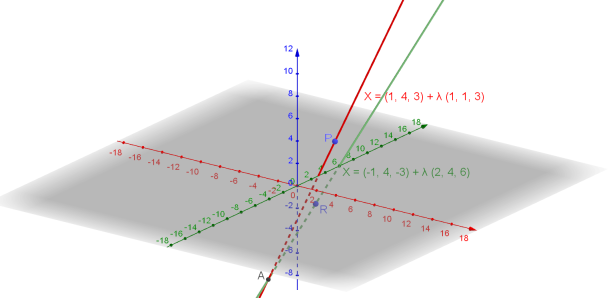
Damit haben wir den Schnittpunkt ausgerechnet. Das gleiche Ergenis erhältst du, wenn du die Gerade h verwendest und den Wert für μ einsetzt. Und damit das vielleicht ein wenig deutlicher wird, habe ich hier noch ein Bild dieser Situation. Wir können die beiden Stützpunkte P und R sowie den Schnittpunkt A der beiden Geraden sehen:
So, das soll es jetzt mit dem Arbeiten mit Geraden gewesen sein. Ganz verlässt uns das nocht nicht, aber die Hauptüberschrift wird dann das Arbeiten mit Ebenen sein.