Bevor wir hier Ernst machen, müssen wir noch zwei Begrifflichkeiten klären nämlich die des Orts- und Richtungsvektors. Kommen wir zuerst zum
Ein Ortsvektor geht immer vom 0-Punkt des Koordinatensystems aus. Jeder(!) Punkt im Koordinatensystem – egal ob im Raum oder in der Ebene – ist durch genau einen Ortsvektor definiert. Dadurch folgt automatisch, dass Ortsvektoren nicht verschiebbar und skalierbar (in der Größe veränderbar) sind. Bei Orstvektoren wird häufig zusätzlich eine 0 vor die Vektorbezeichnung gesetzt. Der Ortsvektor
\[\vec{0u} = \begin{pmatrix} -1 \\-3 \\2 \end{pmatrix}\]
erreicht vom Ursprung aus den Punkt A ( – 1 | – 3 | 2). Mehr geht nicht…
Ein Richtungsvektor ist die Verbindung der Endpunkte zweier Ortsvektoren. Er ist beliebig verschiebbar und skalierbar.
Okay, wie gehen wir damit um? Ganz einfach. Wir nehmen uns zwei Punkte A (1 | 4 | 3) und B (2 | 5 | 6) vor. Die beiden Punkte kann ich durch die Ortsvektoren
\[\vec{0u} = \begin{pmatrix} 1 \\4 \\3 \end{pmatrix} ~und~~ \vec{0v} = \begin{pmatrix} 2 \\5 \\6 \end{pmatrix}\]
darstellen. Den Richtungsvektor von A nach B bestimmen wir, wie wir das im Kapitel „Definition“ schon kennengelernt haben:
\[\vec{w} = \begin{pmatrix} {2 - 1} \\{5 - 4} \\{6 - 3} \end{pmatrix} = \begin{pmatrix} 1 \\1 \\3 \end{pmatrix}\]
So, das wären die Vorüberlegungen, bei denen es nur um Begrifflichkeiten ging. Mehr ist das nicht. Kommen wir nun zum eigentlichen Kapitel:
Wir können mit Hilfe der Vektorrechnung auch Geraden – selbst im 3D-Raum – darstellen und sogar Ebenen. Auch hier versuche ich mich zunächst an das "Überlebenswichtige" zu halten. Für tiefergehende Betrachtungen wird es noch ein zusätzliches Kapitel geben. Hier geht es im Wesentlichen nur darum: wie stellen wir Geraden- und Ebenengleichungen mit dem bisherigen Handwerkszeug auf. Auf geht's mit den
Um eine Gerade eindeutig festzulegen, brauche ich zwei Punkte. Das haben wir in der SI schon gelernt. Übertragen wir das auf die Vektorrechnung folgt: ich brauche einen Punkt (den sogenannten Stützpunkt der Geraden), den ich mit einem Ortsvektor abbilden kann. Dann brauche ich einen zweiten Punkt, um die Richtung der Geraden eindeutig festzulegen. Aus diesen beiden Punkten bilde ich dann den Richtungsvektor. Da ich alle möglichen Punkte auf der Geraden darstellen muss, wird der Richtungsvektor noch mit einer (reellen) Zahl multipliziert. Dadurch schaffe ich es wirklich, alle Punkte auf der Geraden zu erreichen.
Nun gut, stürzen wir uns am besten in die Praxis, dann fällt es leichter. Bleiben wir zunächst in der Ebene. Gegeben sind der Startpunkt A (1 | 1) und ein zweiter Punkt B (2 | 3). Der Richtungsvektor ist dann – wie wir das schon kennengelernt haben:
\[\vec{u} = \begin{pmatrix} {2 - 1} \\{3 - 1} \end{pmatrix} = \begin{pmatrix} 1 \\2 \end{pmatrix}\]
Der Stützpunkt A ist wichtig, da wir die Gerade ja nicht beliebig verschieben können. Die muss schon durch A verlaufen. Daraus ergibt sich die komplette Geradengleichung für die Gerade g:
\[g: ~ \vec{x} = \begin{pmatrix} 1 \\1 \end{pmatrix} + \lambda \begin{pmatrix} 1 \\2 \end{pmatrix}\]
In Worten: von A ausgehend verlaufen beliebige Vielfache des Richtungsvektors. Für Leute, die es genauer wissen möchten: Hier handelt es sich in kartesischer Schreibweise um die Gerade: \(y = 2x – 1\).
Eine wichtige Kleinigkeit noch: Es gibt zwei Möglichkeiten, die Vielfachen von Richtungsvektoren zu benennen. Die eine ist die mit griechischen Buchstaben, angefangen mitλ, die zweite, modernere ist die mit kleinen lateinischen Buchstaben, beginnend mitr. Auch hier gilt: aufpassen, welches Hobby euer Mathelehrer hat. 😉
So, das Ganze geht natürlich auch in 3D:
Wir nehmen uns zwei Punkte A (1 | 4 | 3) als Startpunkt und Stützvektor und B (2 | 5 | 6) für die Richtung. Den Richtungsvektor von A nach B bestimmen wir, wie üblich:
\[\vec{w} = \begin{pmatrix} {2 - 1} \\{5 - 4} \\{6 - 3} \end{pmatrix} = \begin{pmatrix} 1 \\1 \\3 \end{pmatrix}\]
Der Punkt A bleibt wie oben erhalten und damit hat die Gerade die Gleichung:
\[g: ~ \vec{x} = \begin{pmatrix} 1 \\4 \\3 \end{pmatrix} + \lambda \begin{pmatrix} 1 \\1 \\3 \end{pmatrix}\]
Hier die Gerade noch mal als Bild:
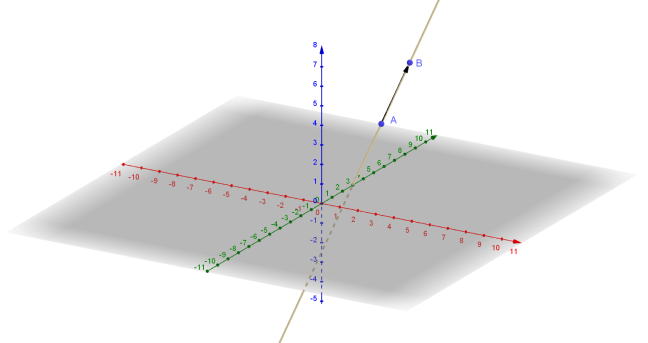
Das geht doch ganz gut! 😊. Das soll es mit den Geraden auch erst einmal sein. Kommen wir noch zu den
Um eine Ebene eindeutig festzulegen, brauche ich genau drei Punkte. Ein einfaches Beispiel aus dem Alltag: ein dreibeiniger Stuhl kann nie wackeln! Alle drei Beine stehen immer fest auf dem Untergrund (der nichts anderes als eine Ebene ist). Wenn wir es mathematisch ganz genau nehmen, müssen wir überprüfen, ob die drei Punkte nicht alle auf einer Geraden liegen (kollinear sind). Des Weiteren müssten wir überprüfen, ob die Richtungsvektoren linear unabhängig (nicht parallel – Skalarprodukt) sind. Das setzen wir hier aber einfach voraus. Da wir eine Ebene auch nicht frei bewegen dürfen, brauchen wir hier ebenfalls einen Stützvektor. Im Gegensatz zur Geraden benötige ich nun zwei Richtungsvektoren, die die Ebene aufspannen. Alle Punkte der Ebene erreiche ich mit Vielfachen beider Richtungsvektoren. Bevor das zu kompliziert wird, nehmen wir uns gleich ein Beispiel vor:
Wir nehmen die drei Punkte A (1 | 4 | 3) als Startpunkt und Stützvektor (in der Abbildung unten: gelb), B (2 | 5 | 6) und C (5 | 4 | 2) für die Richtungen. Den Richtungsvektor von A nach B bestimmen wir, wie wir das oben schon gemacht haben:
\[\vec{u} = \begin{pmatrix} {2 - 1} \\{5 - 4} \\{6 - 3} \end{pmatrix} = \begin{pmatrix} 1 \\1 \\3 \end{pmatrix}\]
Den Richtungsvektor von A nach C bestimmen wir, wie wir nach:
\[\vec{v} = \begin{pmatrix} {5 - 1} \\{5 - 4} \\{2 - 3} \end{pmatrix} = \begin{pmatrix} 4 \\0 \\-1 \end{pmatrix}\]
Damit sind wir fast fertig. Wir müssen das wieder zusammensetzen und erhalten:
\[E: ~ \vec{x} = \begin{pmatrix} 1 \\4 \\3 \end{pmatrix} + \lambda \begin{pmatrix} 1 \\1 \\3 \end{pmatrix} + \mu \begin{pmatrix} 4 \\0 \\-1 \end{pmatrix} \]
In der 3D-Darstellung sieht das Ganze dann so aus:
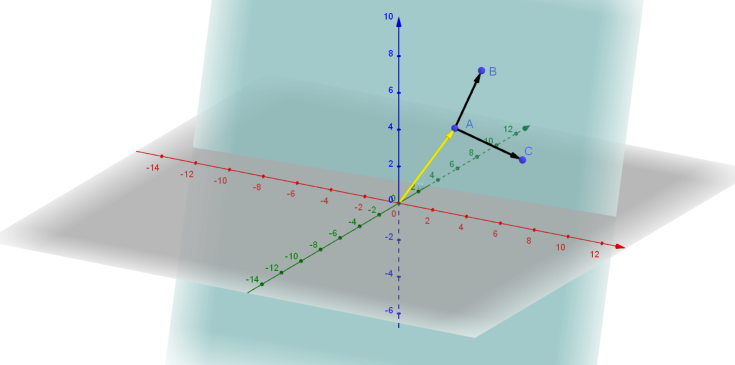
Wir sehen, das ist zwar ungewohnt aber gar nicht so kompliziert. Wir erweitern sozusagen einen Ortsvektor zur Geraden und die zur Ebene 😉 . Das war’s schon 😊. Und damit können wir wirklich leichter rechnen, als wenn wir mit x, y und z arbeiten würden… Spätestens bei den Ebenen macht sich die Einfachheit der Vektoren bemerkbar.
Das soll so weit als Einführung reichen. Was kann man noch machen?
Einiges davon werden ich noch in einem Extra-Kapitel behandeln. Aber mit dem Grundsätzlichen soll hier erst einmal Schluss sein. 😊