Nachdem wir kennengelernt haben, was Vektoren sind und wie man sie zeichnet, geht es in diesem Kapitel um das Rechnen mit Vektoren. Auch hier soll eher eine Einführung stehen als eine in die Tiefe gehende Betrachtung. Ein bisschen Arbeit will ich euren Lehrern ja auch noch lassen 😉. Aber keine Angst. Ich denke, nach diesem Kapitel seid ihr so weit fit, dass ihr dem Rest folgen könnt. Bevor wir zur eigentlichen Addition kommen, brauchen wir noch etwas vorweg, nämlich den
Den Betrag eines Vektors (oder im umgangssprachlichen: die Länge eines Vektors) können wir ganz einfach ausrechnen. Erinnern wir uns dran, wie wir in der Einführung den Vektor
\[\vec{u} = \begin{pmatrix} 2 \\4 \end{pmatrix}\]
gezeichnet haben.
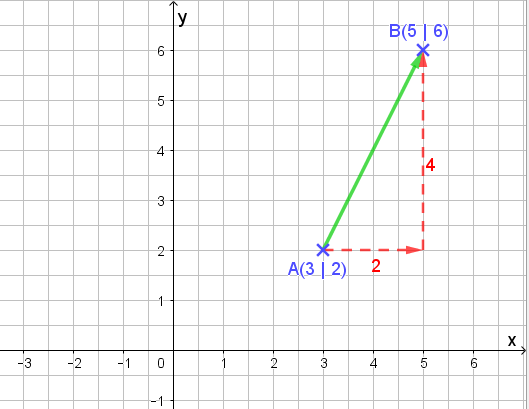
Schauen wir uns die rot-gestrichelten Linien an und den Vektor. Zusammen bilden sie ein rechtwinkliges Dreieck mit den Katheten der Länge 2 und 4. Da wir die Katheten kennen, können wir die Länge des Vektors ganz einfach mit Hilfe des Satzes von Pythagoras ausrechnen:
\begin{align} u^2 &= 2^2 + 4^2\\ u &= \sqrt{2^2+4^2}\\ u &= \sqrt{20} = 4\sqrt5 \end{align}
Super! 😊 Bislang haben wir mit konkreten Zahlen gearbeitet. Aber der Mathematiker wäre nicht Mathematiker, wenn er das nicht allgemein aufschreiben würde 😉. Für die allgemeine Schreibweise gibt es (natürlich – seufz) mehrere Möglichkeiten. Ich wähle hier eine, die uns das Leben (hoffentlich) etwas einfacher macht – insbesondere für das, was noch kommt.
Jeder Vektor hat ja eine Bezeichnung. Diese wird in der Komponentenschreibweise wieder verwendet. Als Index kommt dann die jeweilige Achsenrichtung dazu. Damit das jetzt nicht zu kompliziert klingt:
\[\vec{u} = \begin{pmatrix} u_x \\u_y \end{pmatrix}\]
bei einem Vektor in der Ebene und
\[\vec{u} = \begin{pmatrix} u_x \\u_y \\u_z \end{pmatrix}\]
bei einem dreidimensionalen Vektor.
Damit verallgemeinert sich die Berechnung des Betrags zu
\[\vert\vec{u}\vert = \sqrt{u_x^2+u_y^2}\]
bei einem Vektor in der Ebene und
\[\vert\vec{u}\vert = \sqrt{u_x^2 + u_y^2 + u_z^2}\]
bei einem Vektor im Raum.
Okay, das kriegen wir hin. Was können wir noch machen? Wir können Vektoren addieren.
Machen wir das zunächst zeichnerisch.Hier sieht das so aus, dass wir den Anfangspunkt des zweiten Vektors auf den Endpunkt des ersten Vektors legen. Jetzt verbinden wir den Anfangspunkt des ersten Vektors mit dem Endpunkt des 2. Vektors. Wir erhalten somit einen neuen Vektor.
Machen wir das Schritt für Schritt: Ich habe die beiden Vektoren
mit ihren jeweiligen Start- und Richtungspunkten.
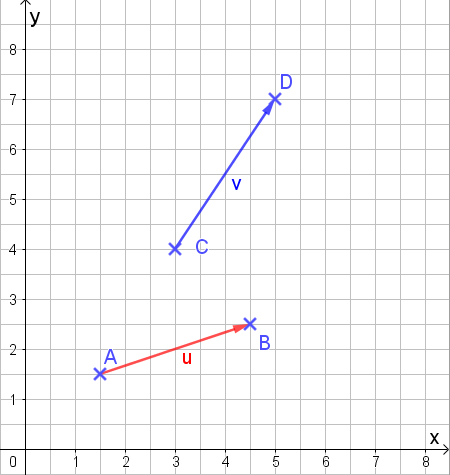
Jetzt schieben wir den Punkt C auf den Punkt B.
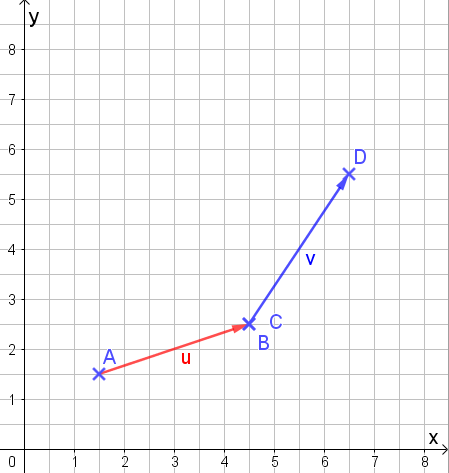
Jetzt verbinden wir A und D zu einem Vektor in Richtung D:
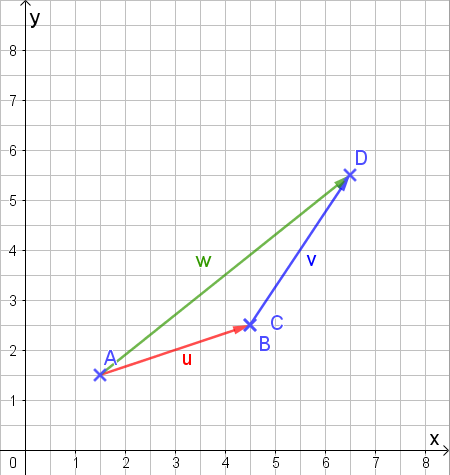
Wenn wir uns die Komponenten des neuen Vektors anschauen, müssen wir vom Anfangspunkt A 5 Einheiten nach rechts in x-Richtung gehen und 4 Einheiten senkrecht nach oben in y-Richtung, um ihn vollständig zu beschreiben.
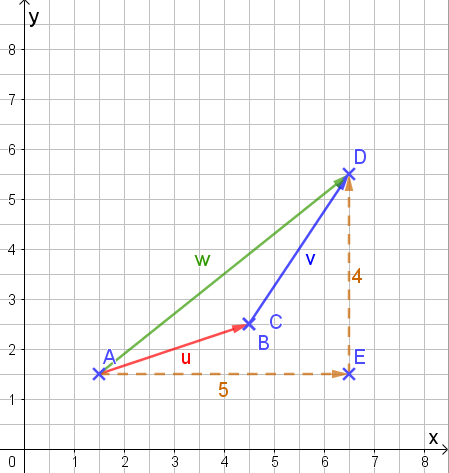
Der neue Vektor ist also definiert als
\[\vec{w} = \begin{pmatrix} 5 \\4 \end{pmatrix}\]Das Ganze geht natürlich auch rechnerisch. Schauen wir uns dazu die Komponenten der Vektoren an:
\[{u_x = 3, v_x = 2~und~ w_x = 5}\]
\[{u_y = 1, v_y = 3~und~ w_y = 4}\]
Offenbar erhalten wir die x-Komponente des neuen Vektors aus der Addition der x-Komponenten der beiden Ausgangsvektoren (3 + 2). Dasselbe gilt auch für die y-Komponenten (1 + 3). Super! Das ist es! Genauso machen wir das bei der Addition zweier Vektoren. Wir addieren die jeweiligen x-, y- (und z-) Komponenten, wenn wir schriftlich rechnen. Das ist nicht schwer… 😊. Dasselbe gilt natürlich auch für dreidimensionale Vektoren. In allgemeiner Schreibweise sieht das für einen dreidimensionalen Vektor daher so aus:
\[\vec{w} = \vec{u} + \vec{v} = \begin{pmatrix} {u_x + v_x} \\{u_y + v_y} \\{u_z + v_z} \end{pmatrix}\]Bei einem zweidimensionalen Vektor fällt die z-Komponente weg.
Ein Beispiel schauen wir uns noch dazu an: Addiere die beiden Vektoren
Super! Da haben wir schon Schwierigeres gemacht… 😉
Damit kommen wir schon zur
Die Subtraktion von Vektoren ist im Prinzip genauso einfach, wie deren Addition. Wir müssen aber aufpassen welchen Vektor wir von welchem abziehen. Das ist aber bei ganzen Zahlen dasselbe. Ob ich nun rechne 3 – 2 oder 2 – 3 macht einen gewaltigen Unterschied. Die Ergebnisse sind nicht identisch. Genauso ist das auch bei Vektoren, also nicht wirklich etwas Neues.
Nehmen wir gleich ein konkretes Beispiel: Wir haben wieder die beiden Vektoren
\[\vec{u}=\begin{pmatrix} 3 \\1 \end{pmatrix}und\ \vec{v}=\begin{pmatrix} 2 \\3 \end{pmatrix}\]aus unserem obigen Beispiel und berechnen
\[\vec{w} = \vec{v} - \vec{u}\]Geometrisch verfahren wir nun so, dass wir beide Anfangspunkte (A und C) zusammenfallen lassen. Der Ergebnisvektor verläuft dann von B nach D. Die Pfeilspitze des Ergebnisvektors zeigt bei der Subtraktion immer in Richtung des Vektors, von dem wir subtrahieren.
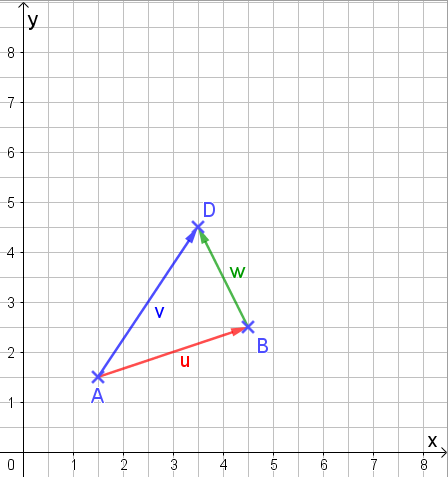
Wieso ist das nun eine Subtraktion? Ganz einfach: wenn ich von D über A nach B gehe, wechsele ich in A die Pfeilrichtung. Die umgekehrte Pfeilrichtung drückt das negative Vorzeichen aus. Rechnerisch ist das genauso wie bei der Addition:
\[\vec{w} = = \vec{v} - \vec{u} = \begin{pmatrix} {2 - 3} \\{3 - 1} \end{pmatrix} = \begin{pmatrix} - 1 \\2 \end{pmatrix}\]Die Subtraktion von Vektoren ist damit grundsätzlich nicht schwieriger als die Addition. Wir müssen uns nur Gedanken um die richtige Reihenfolge machen, wie bei der „normalen“ Subtraktion auch.
Bei der Subtraktion und Addition von Vektoren kann ich nur solche addieren/subtrahieren, die die gleiche Anzahl von Komponenten haben!
\[\vec{c} = \begin{pmatrix} 3 \\5 \end{pmatrix} + \begin{pmatrix} 1 \\7 \end{pmatrix}\]kann ich addieren,
\[\vec{c} = \begin{pmatrix} 3 \\5 \end{pmatrix} + \begin{pmatrix} -6 \\-6 \\8 \end{pmatrix}\]kann ichnicht addieren!
Okay. Bis jetzt, so hoffe ich, kann man das ganze nachvollziehen und umsetzen. Gönnen wir uns ein wenig Pause, bevor wir uns mit der Multiplikation von Vektoren beschäftigen…