Du hast mit Sicherheit schon einmal in einen Spiegel geschaut. Da sind dir vielleicht schon bestimmte Dinge aufgefallen, wie z.B. die Spiegelschrift. Im Folgenden werden wir ein paar Dinge unter die Lupe nehmen und sehen, wie wir das in der Ebene konstruieren können.
Schaue dir folgendes Bild an:

Vor dem Spiegel ist ein Punkt. Du siehst diesen Punkt auch hinter dem Spiegel. Wenn wir die Karokästchen zählen, sehen wir, dass wir vor dem Spiegel 6 Karokästchen vom Punkt bis zum Spiegel haben. Im Spiegel sind genauso viele Karokästchen vom Spiegel bis zum Punkt zu sehen.
Das bringen wir jetzt in eine Zeichnung. Den Spiegel ersetzen wir dabei durch die sogenannte Spiegelachse S. Das wäre die Linie, wo der Spiegel das Papier berührt. Den Punkt nenne wir A.
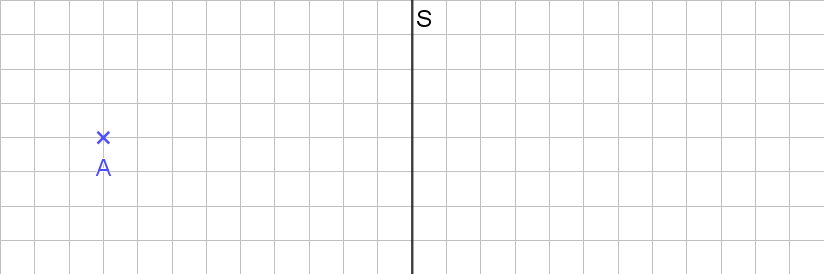
Jetzt geht es darum, den Punkt hinter dem Spiegel zu finden. Wir nehmen den kürzesten Weg (grüne Linie) zur Spiegelachse (wir wissen schon, dass das eine Senkrechte ist) und verlängern über die Spiegelachse hinaus um die gleiche Länge (rote Linie). Dort erhalten wir dann den Punkt A‘. Der Strich sagt uns, dass das der Bildpunkt ist, also der Punkt, den wir im Spiegel sehen würden. Das Ganze sieht dann so aus:
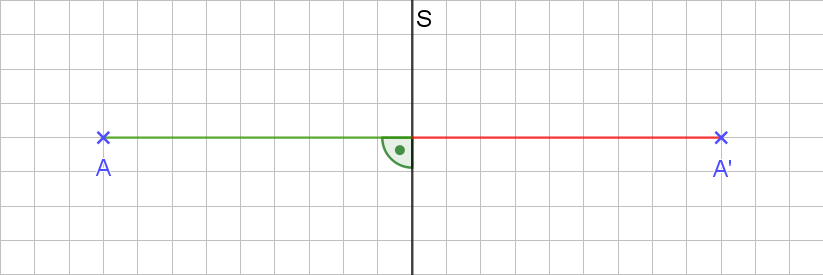
Mit A‘ haben wir das Spiegelbild des Punktes A nun konstruiert. Damit wir nicht immer Kästchen zählen müssen, nehmen wir zur Konstruktion unser Geodreieck. Das kommt mit der Mittellinie auf die Spiegelachse. Damit haben wir schon automatisch den rechten Winkel. Dann messen wir die Entfernung des Punktes A bis zur Spiegelachse und zeichnen den Bildpunkt A‘ dann in derselben Entfernung auf der anderen Seite der Spiegelachse.
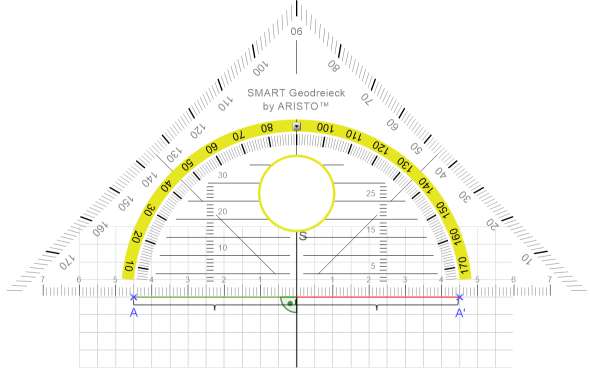
Natürlich können wir das auch mit mehreren Punkten machen. Wenn wir Figuren auf diese Weise spiegeln, machen wir das nämlich über die Eckpunkte. Nehmen wir uns einmal ein einfaches Dreieck vor.
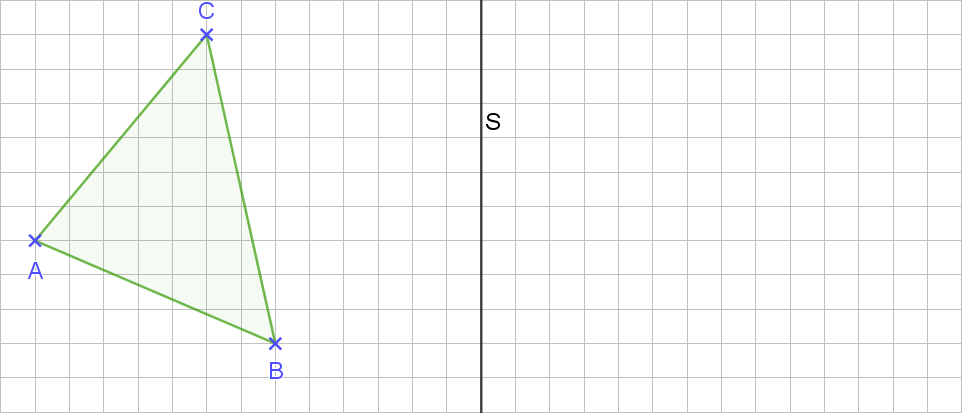
Wir verfahren jetzt mit allen drei Eckpunkten so, wie mit dem Punkt A vorhin. So erhalten wir nacheinander die Bildpunkte A‘, B‘ und C‘. Wir verbinden dann A‘, B‘ und C‘ und erhalten dann das gespiegelte Dreieck.
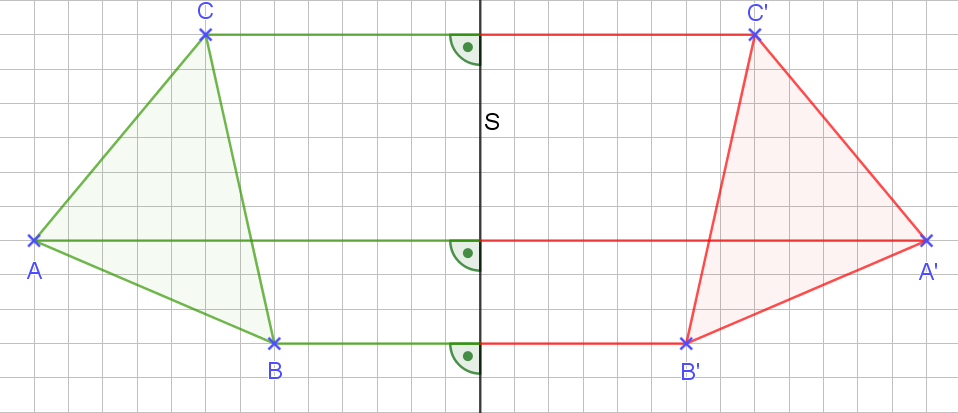
Das ist doch gar nicht schwer… 😉
Was mit drei Ecken geht, sollte auch mit fünf gehen…
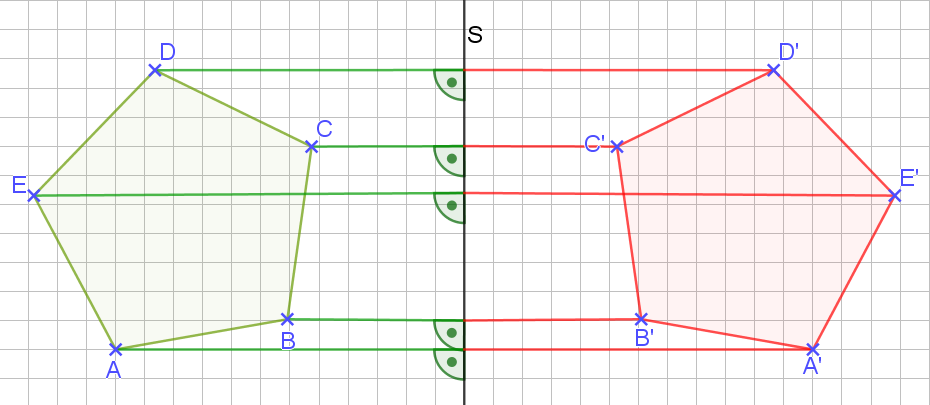
Super. Das kriegen wir hin. 😊 Bislang lag die Spiegelachse immer außerhalb der Figur. Was machen wir aber, wenn die Spiegelachse die Figur schneidet??? Kein Problem! Wir machen das Gleiche wie vorher! Wir gehen konsequent von den Eckpunkten der Figur – egal ob von rechts oder von links – senkrecht zur Spiegelachse, verlängern die Strecke um den gleichen Betrag und erhalten den entsprechenden Bildpunkt. Das sieht dann bei einem Dreieck beispielsweise so aus:
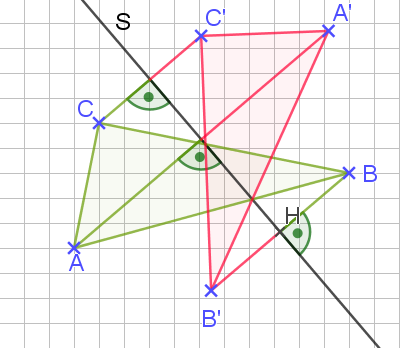
Also: zwar etwas ungewohnt, aber alles im grünen Bereich! 😊
Jetzt wollen wir die Eigenschaften noch ein wenig in Bewegung untersuchen. Dazu habe ich euch ein Arbeitsblatt fertig gemacht und ein paar Aufgaben dazu.
Wer gut mit der Lösung der vorherigen Aufgaben klarkommt, kann sich noch einmal hier versuchen. Das sieht zwar ähnlich aus, wird aber ein wenig schwieriger.
So, nun haben wir einiges über Spiegelungen gelernt. Was ich euch nicht abnehmen kann, ist das Konstruieren mit dem Geodreieck. Aber wenn man einmal den Bogen raus hat und sorgfältig arbeitet, dann wird man keine Probleme haben. Und das kriegt ihr doch hin - oder ... ?! 😊