Im rechtwinkligen Dreieck haben wir ja schon eine Menge über die Beziehungen von Seiten kennengelernt, nämlich über die Satzgruppe des Pythagoras. Aber das ist ja auf rechtwinklige Dreiecke beschränkt. Da tut sich die Frage auf, ob es denn nicht auch etwas für „normale“ Dreiecke gibt. Und die Antwort lautet: Na klar! Es gibt sogar zwei Möglichkeiten, und zwar den Sinussatz und den Kosinussatz. Ich werde beide hier herleiten (was auch nicht besonders dramatisch ist). Mit beiden haben wir dann die Möglichkeit, fehlende Seiten oder auch Winkel auszurechen.
Okay, nehmen wir uns ein allgemeines DreieckABC vor mit α, β und γ ≠ 90°:
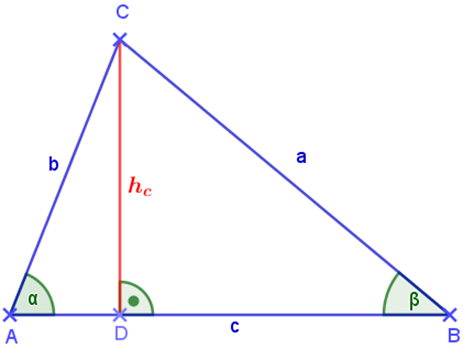
Damit wir vernünftig arbeiten können, habe ich noch \(h_c\) eingezeichnet. Dadurch erhalten wir zwei rechtwinklige Dreiecke, nämlichADC undDBC. Fangen wir mit dem linken an:
Der Winkel α ist bekannt. Dann kann ich den Sinus des Winkels bestimmen, nämlich:
\[sin~\alpha~=~{{h_c}\over {b}}\]
Soweit nicht schwer – oder? Dasselbe machen wir mit dem zweiten Teildreieck, in dem β gegeben ist:
\[sin~\beta~=~{{h_c}\over {a}}\]
Wir sehen nun, in beiden Ausdrücken kommt \(h_c\) vor. Lösen wir beide Gleichungen nach \(h_c\) auf:
\(b \cdot sin~ \alpha = h_c\)und
\(a \cdot sin~ \beta = h_c\)Super! Wir setzen gleich und erhalten:
\(b \cdot sin~ \alpha = a \cdot sin~ \beta\)Wir sortieren noch ein bisschen um und sehen:
\[{{sin~\alpha} \over {a}}~=~{{sin~\beta}\over {b}}\]
Wenn wir im gleichen Dreieck noch mit \(h_a\) arbeiten statt mit \(h_c\) bekommen wir:
\[{{sin~\gamma} \over {c}}~=~{{sin~\beta}\over {b}}\]
Damit erhalten wir insgesamt:
\[{{sin~\alpha} \over {a}}~=~{{sin~\beta}\over {b}}~=~{{sin~\gamma} \over {c}}\]
Und genau das ist der Sinussatz. Das heißt, ich kann über die Winkel (genauer deren Sinus) fehlende Seitenlängen ausrechnen. Das ist außerordentlich praktisch. Bei vielen Vermessungen im Gelände können wir nun munter drauf losarbeiten, ohne dass wir uns um die Einrichtung eines rechten Winkels kümmern müssen 😉. Aber natürlich brauchen nicht nur die Vermessungstechniker den Sinussatz. Wann immer fehlende Strecken oder Winkel zu bestimmen sind, ist der Sinussatz ein gutes Mittel der Wahl.
So, kommen wir nun zum zweiten Teil, nämlich der
Gegeben sind 2 Seiten eines beliebigen Dreiecks und der von ihnen eingeschlossene Winkel, z.B.b, c und α ≠ 90°.
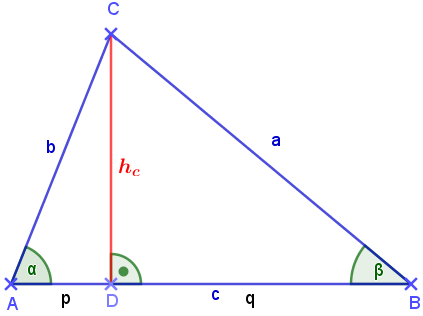
Nehmen wir wieder das Dreieck, das wir gerade schon hatten. Die Höhe \(h_c\) zerlegt unser Dreieck ja in zwei rechtwinklige Dreiecke und die Seitec in die Abschnittep undq.
Im DreieckADC gilt:
\[sin~\alpha~=~{{h_c}\over {b}}~\Rightarrow~ h_c ~=~ {\color{dodgerblue}{b \cdot sin~\alpha~~(1)}}\]Das kennen wir schon. Im selben DreieckADC können wir aber auch die Strecke p berechnen:
\[cos~\alpha~=~{{p}\over {b}}~\Rightarrow~ p ~=~ {\color{red}{b \cdot cos~\alpha~~(2)}}\]Nun sehen wir uns das zweite TeildreieckDBC an und stellen dort den Satz des Pythagoras auf. Er liefert uns folgende Gleichung:
\[a^2 ~=~ h_c^2~+~ q^2 ~~(3)\]Okay, \(~h_c\) haben wir schon bei (1) ausgerechnet. Es fehlt noch \(q\). Wir wissen:
\(p + q = c\)
oder
\(q = c - p\)
\(p\) haben wir ja bei (2) ausgerechnet, also ergibt sich:
\(q = c - \color{red} {b \cdot cos~ \alpha~~(4)} \)
Nun ersetzen wir in Gleichung (3) \(~h_c\) durch das Ergenis ausGleichung (1) undq durch das Ergebnis ausGleichung (4):
\(a^2 = {\color{dodgerblue} {(b \cdot sin~\alpha)^2}} + \color{red} {(c - b \cdot cos~ \alpha)^2} \)
Wenn wir die Klammern auflösen (Achtung! Beim zweiten Teilterm die 2. binomische Formel beachten!) ergibt sich:
\(a^2 = {\color{dodgerblue} {b^2 \cdot sin^2~\alpha}} + \color{red} {c^2 - 2bc \cdot cos\ \alpha + b^2 \cdot cos^2~ \alpha} \)
Das sortieren wir noch ein wenig um:
\(a^2 = {b^2 \cdot (\color{dodgerblue} {sin^2~\alpha~}+ \color{red} {cos^2~ \alpha}}) + \color{red} {c^2 - 2bc \cdot cos\ \alpha} \)
Wir müssen jetzt nur noch wissen (kann man in jeder einschlägigen Formelsammlung nachschlagen), dass gilt:
\(sin^2~ \alpha + cos^2~ \alpha = 1\)
Dann vereinfacht sich das Ganze zu:
\(a^2 = b^2 + c^2 - 2 b c \cdot cos~ \alpha \)
Fertig! Super! Das ist der Kosinussatz! Wir finden also auch in jedem beliebigen Dreieck eine Beziehung zwischen den Seiten, nicht nur beim Pythagoras. Entsprechend gilt für die anderen Seiten:
\(b^2 = a^2 + c^2 - 2 a c \cdot cos~ \beta \)
\(c^2 = a^2 + b^2 - 2 a b \cdot cos~ \gamma \)
Der Kosinussatz gilt dabei für jedes beliebige Dreieck. Ich muss nur zwei Seiten und den von ihnen eingeschlossenen Winkel kennen, um die dritte Seite zu bestimmen.
Für Spezialisten: Wenn wir uns den letzten Term ansehen und für γ = 90° einsetzen, so wird cos γ gleich 0. Damit wird der gesamte Teilterm 0 und wir erhalten die Grundform des Satzes von Pythagoras, nämlich
\(c^2 = a^2 + b^2 \)
Damit können wir den Pythagoras auch als Spezialfall des Kosinussatzes auffassen 😉