Bislang haben wir ja ausschließlich lineare Funktionen kennengelernt, wie z.B. \(y = x\). Hier hat der Exponent den Wert 1. Weitere Formen waren z.B. \(y = 3 x + 5\). Linear haben wir diese Funktionen deshalb genannt, weil ihr Schaubild eine Gerade darstellt. Wie sieht das nun aber aus, wenn ich nicht 1 sondern 2, 3, 4… als Exponent habe? Machen wir uns doch mal eine Wertetabelle für \(y = x^2\) und tragen die Punkte in ein Koordinatenkreuz ein:
| \(x\) | – 3 | – 2 | – 1 | 0 | 1 | 2 | 3 |
| \(y\) | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
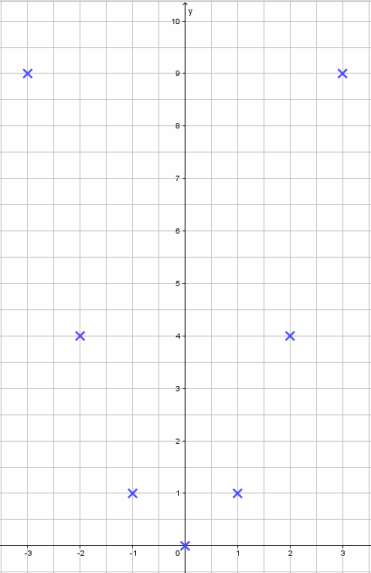
Wir sehen, die Punkte liegen nicht auf einer Geraden. Verbinden wir alle Punkte, so erhalten wir folgendes Schaubild:
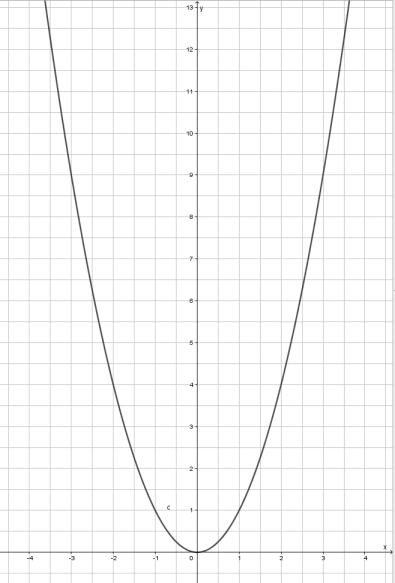
Diese Form nennen wir eine Parabel – und weil das die einfachste Form ist auch „Normalparabel“. Den tiefsten Punkt (hier bei 0|0) nennen wir Scheitelpunkt der Parabel.
Es taucht natürlich gleich die Frage auf: Ist das jetzt wieder nur ein Spielkind der Mathematik? Mitnichten!

Brückenbögen z.B. haben die Form einer Parabel, weil sie so die Kräfte bei Belastung am besten ableiten können.

lizensiert gemäß CC BY-SA
Beim Freiwurf beim Basketball beschreibt der Ball eine Parabelbahn.
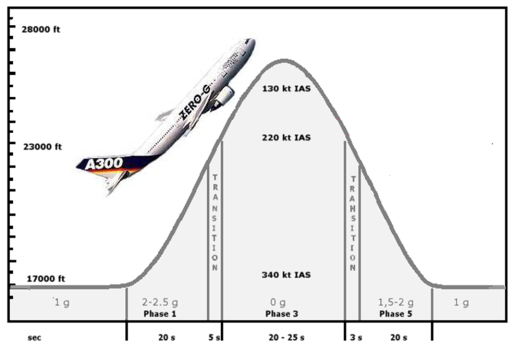
lizensiert gemäß CC BY-SA
Beim schwerkraftlosen Flug zum Training von Astronauten beschreibt das Flugzeug eine Parabelbahn.

Ein Wasserstrahl beschreibt eine Parabelbahn…
Diese ganzen Beispiele zeigen: Wir können mit Parabeln offensichtlich eine ganze Menge anfangen. Also lohnt es sich durchaus, sich damit zu beschäftigen. Okay, machen wir das und kommen zu
Dazu habe ich ein kleines Arbeitsblatt vorbereitet. Wenn du den Schieberegler ziehst (das kannst du mit der Maus machen, dem Finger beim Tablet oder du nimmst auf der Tastatur die Pfeiltasten – dann geht es schön langsam). Du wirst sehen, die Form der Parabel verändert sich. Zum Vergleich ist die Normalparabel immer sichtbar.
Fassen wir zusammen:
Kommen wir zum nächsten Fall, nämlich:
Auch hierzu habe ich wieder ein Arbeitsblatt, wie oben schon beschrieben. Probiere aus, was passiert, wenn ich über den Schieberegler b verändere.
Fassen wir wieder zusammen:
Damit wären wir auch schon beim dritten Fall, nämlich
Probiere wieder beim Arbeitsblatt aus, wie sich die Parabel verändert, wenn ich c verändere:
Fassen wir zusammen:
Okay, das war doch gar nicht so schwer. Jetzt kombinieren wir das Ganze und erhalten:
Nutze auch hier wieder mein Arbeitsblatt und verändere alle drei Elemente \(a\), \(b\) und \(c\).
Fassen wir zusammen:
Deswegen nennt sich diese Form der Parabelgleichung auch allgemeine Parabelgleichung, und zwar in der sogenanntenScheitelpunktform. In der Scheitelpunktform (zur anderen kommen wir gleich) können wir auf einen Blick den Scheitelpunkt der Parabel ablesen. Der liegt nämlich bei \(S (b~ |~ c)\). Wir können sehen, ob die Parabel nach oben oder unten geöffnet ist und ob sie gestreckt oder gestaucht ist. Wir können also Aussagen machen über die
Nehmen wir uns auch hier gleich ein Beispiel vor:
\[y = (x – 3)^2 + 4\]Wir sehen: \(a = 1\), das heißt es handelt sich um eine Normalparabel. \(b = 3\) und \(c = 4\). Also liegt der Scheitelpunkt bei \(S (3~ |~ 4)\).
\[y = - 3 (x + 4)^2 - 5\]Wir sehen: \(a = - 3\), das heißt es handelt sich um eine um eine nach unten geöffnete, gestreckte Parabel. \(b = - 4\) (achte auf das Vorzeichen von \(b\) in der Klammer!) und \(c = - 5\). Also liegt der Scheitelpunkt bei \(S (- 4 ~|~ - 5)\).
Du schaffst es doch bestimmt, mit dem letzten interaktiven Arbeitsblatt diese Parabeln darzustellen! Probiere es aus! Dann siehst du noch einmal genau, was die Parameter einer Parabelgleichungen bedeuten.
Umgekehrt kann man bei einer Normalparabel
Auch hierzu ein kleines Beispiel:
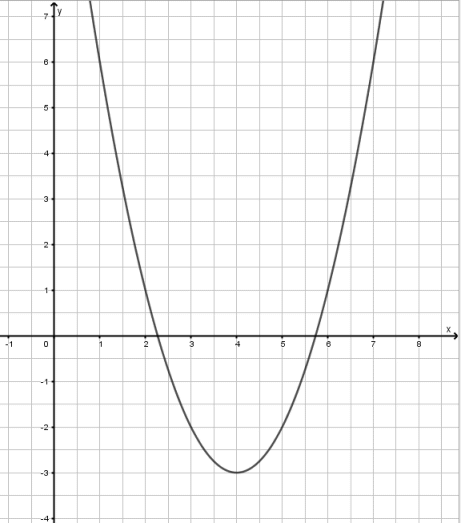
Der Scheitelpunkt liegt bei \(S (4~ | ~– 3)\). Das setzen wir in die allgemeine Parabelgleichung ein:
\[y = a (x – b)^2 + c\]Normalparabel heißt: \(a = 1\). \(b\) ist 4 und \(c\) ist – 3. Also:
\[y = (x – 4)^2 – 3\]Und noch ein zweites Beispiel:
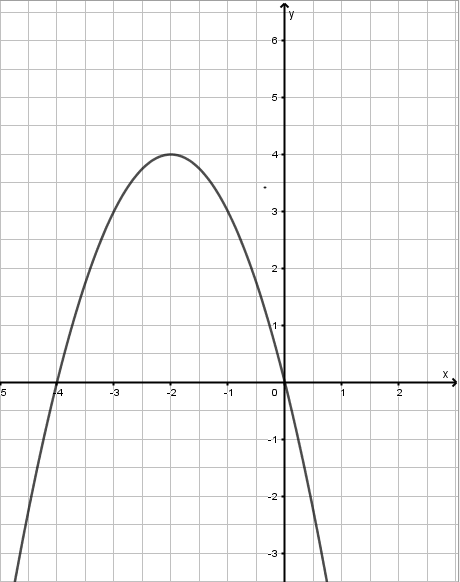
Hier ist die Parabel nach unten geöffnet. Das heißt: \(a = – 1\). Der Scheitelpunkt liegt bei \(S (–2~ |~ 4)\). Damit ist \(b = – 2\) und \(c = 4\). Damit lautet die Parabelgleichung:
\[y = – (x + 2)^2 + 4\]Gar nicht so schwer... Manchmal liegt eine Parabel aber auch in einer anderen Schreibweise vor, nämlich der
Die lautet:
\[\large y = ax^2 + bx + c\]Diese Form hat weniger Bedeutung als die Scheitelpunktform. Auch hier können wir sehen, ob die Parabel gestreckt, gestaucht, nach oben oder unten geöffnet ist \((a)\). Wir sehen auch, dass die Parabel in \(y\)-Richtung \((c)\) verschoben wurde, allerdings können wir nicht exakt den Betrag ablesen. Auch mit der Verschiebung in \(x\)-Richtung tun wir uns mit dieser Form etwas schwer.
Aber zum Glück können wir beide Formen ineinander umformen und sind bei der
Zunächst werden wir das rechnerisch machen, denn das wollen eure Mathelehrer von euch sehen. Am Ende gibt es noch einen kleinen Tipp, wie ihr das auch ohne Rechnen herausbekommt. Das lohnt sich aber auf jeden Fall dennoch, wenn ihr eure Hausaufgaben kontrollieren oder üben möchtet. 😉
Was brauchen wir?
Die Scheitelpunktform einer Parabelgleichung lautet ja ohne Stauchungsfaktor (mit machen wir später):
\[\large y = (x - b)^2 + c\]Das heißt, wir müssen die Normalform so umbasteln, dass wir ein Binom erhalten. Okay… Schreiben wir die zweite binomische Formel (wegen dem Minuszeichen in der Klammer) doch noch einmal auf:
\[\large (a – b)^2 = a^2 – 2 a b + b^2\]oder mit den Termen aus der Parabelgleichung:
\[\large (x – b)^2 = x^2 – 2 x b + b^2\]Warum? Ganz einfach. Wenn wir den mittleren Term kennen und eine der beiden anderen Variablen können wir die zweite ausrechnen. So etwas haben wir früher schon gemacht – und genau das brauchen wir hier. Nehmen wir gleich ein konkretes Beispiel:
\[y = x^2 – 6 x + 5\]In meiner allgemeinen Scheitelpunktform kenne ich \(b\) und \(c\) noch nicht. Das müssen wir ergänzen. Wir gehen folgendermaßen vor:
Zuerst kümmern wir uns nur um die rechte Seite der Gleichung und lassen in der Normalform die + 5 beiseite. Da kümmern wir uns später noch drum. Es bleibt also übrig:
\[x^2 – 6x\]Das ist der vielversprechende Anfang eines Binoms. Den rechten Term muss ich durch 2 und durch \(x\) teilen, damit ich \(b\) bekomme. Machen wir das und es bleibt übrig: 3. Super! \(b\) ist also 3. Damit kann ich schreiben:
\[x^2 – 6x + 3^2 ~~~\text{oder} ~~~x^2 – 6x + 9\]Damit kann ich diesen Term jetzt schreiben als
\[\large (x – 3)^2\]Das hilft schon sehr. Aaaaber ich habe zu meiner Parabel\(\boldsymbol{gleichung}\) 9 addiert. Wir wissen aber, dass ich am Gleichgewicht einer Gleichung (Waage!) nichts verändern darf. Also muss ich gleichzeitig wieder 9 subtrahieren, damit alles im Gleichgewicht bleibt. Das schreibe ich hinter die Klammer – und jetzt kommt die + 5 noch dazu, die ich vorhin beiseitegeschoben habe. Wir erhalten:
\[y = (x – 3)^2 – 9 + 5\]oder
\[\large y = (x – 3)^2 – 4\]Damit haben wir die Normalform
\[y = x^2 – 6x + 5\]in die Scheitelpunktform
\[\large y = (x – 3)^2 – 4\]umgeformt. Ich habe ja am Ende einen Tipp versprochen. Den möchte ich hier jetzt schon geben, und zwar die
Wir starten Geogebra und geben die Gleichung in der Normalform so, wie sie ist, in die Eingabezeile unten ein und beenden die Eingabe mit Enter (wichtig!). Jetzt sehen wir links im Algebrafenster die Funktionsgleichung in der Form:
c: y = x² - 6x + 5
Wir klicken mit derrechten Maustaste auf die Gleichung. Es geht folgendes Menü auf:
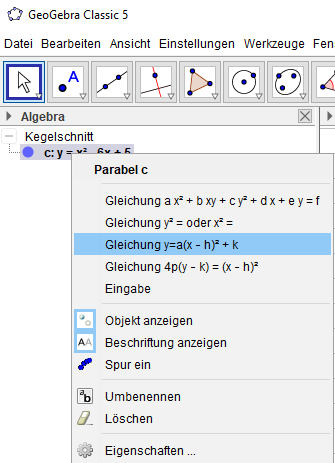
Wir wählen den blau hinterlegten Menüpunkt aus und voilà, die Anzeige im Algebrafenster ändert sich in:
\[c:~ y = (x - 3)^2 - 4\]Das Ganze geht natürlich auch umgekehrt 😉. Steht die Scheitelpunktform im Algebrafenster findet sich die Normalform im Menü an derselben Stelle.
Insgesamt ein sehr nützliches Tool – und vor allem kostenlos 😊.
Was machen wir aber, wenn in der Normalform noch ein Stauchungsfaktor steht? Okay, auch hier ist das Vorgehen im Prinzip dasselbe, wir müssen nur einen Schritt ergänzen:
Befassen wir uns gleich mit einem konkreten Beispiel:
\[\large y = 2x^2 – 12x + 23\]Wie eben kümmern wir uns nur um den rechten Teil und lassen die + 23 erst mal beiseite. Es bleibt also stehen:
\[2x^2 – 12x\]Wir klammern jetzt die 2 aus:
\[2 (x^2 – 6x + …)\]Der Term in der Klammer kommt uns bekannt vor. Den hatten wir gerade schon. Wir wissen, in der Klammer müssen wir 3² (oder auch 9) addieren.
\[2 (x^2 – 6x + 9)\]Und schreiben das dann als:
\[2 (x – 3)^2\]Nun müssen wir nur noch auf den Faktor vor der Klammer aufpassen.In der Klammer haben wir 9 addiert. Durch den Faktor vor der Klammer sind das für die Gleichung aber 2 · 9 = 18! Diesmal müssen wir also 18 wieder subtrahieren, damit die Gleichung stimmt und die 23 von vorhin kommen wieder dazu. Also:
\[y = 2 (x – 3)^2 – 18 + 23\]oder
\[\large y = 2 (x – 3)^2 + 5\]Fertig! Das Ganze geht natürlich auch mit Geogebra, wie gerade beschrieben.
Damit haben wir die wichtigsten Aspekte der Parabeln in Klasse 10 erledigt. 😊
Und wer jetzt noch möchte und neugierig ist, wie die Graphen der Funktionen mit höheren Potenzen aussehen, kann sich hier die Graphen der Funktionen von \(y = x bis y = x^{10} anschauen.