
Kreise spielen in der Mathematik eine ziemlich große Rolle. Zunächst einmal die Frage: Was ist denn nun eigentlich ein Kreis? Ganz einfach: Ein Kreis ist eine Linie, die von einem vorgegebenen Punkt immer den gleichen Abstand hat.

Den Punkt nennen wir Mittelpunkt (M), den Abstand von M zur Kreislinie nennen wir den Radius (r) und die Linie Kreislinie. Das sind halt nur Begriffe, die wir uns merken müssen. Dazu kommt noch ein weiterer, nämlich der Durchmesser (d). Wie unterscheiden sich Radius und Durchmesser? Das ist nicht schwer.
Der Radius ist eine Linie, die den Mittelpunkt mit einem Punkt auf der Kreislinie verbindet.
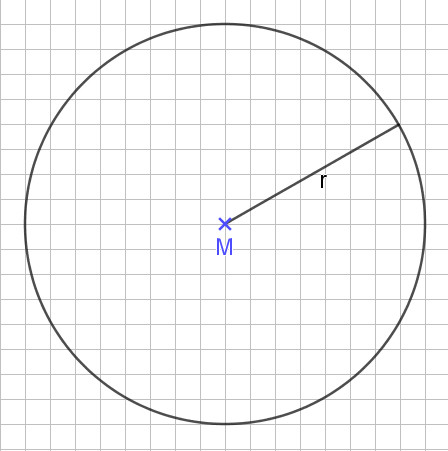
Der Durchmesser ist eine Linie, die zwei Punkte auf der Kreislinie verbindet, wobei sie durch den Mittelpunkt verläuft. Damit ist der Durchmesser auch doppelt so lang wie der Radius:
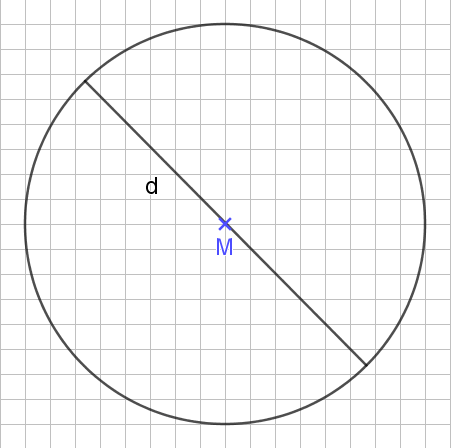
So, nach den Begrifflichkeiten geht es auch schon los. Kreise haben eine besondere Eigenschaft:
Für jeden, aber auch wirklich jeden Kreis gilt: Das Verhältnis von Umfang zu Durchmesser ist kontant. Das heißt in anderen Worten: Bilde ich den Quotienten aus Umfang und Durchmesser (oder auch: teile ich den Umfang durch den Durchmesser), kommt immer exakt der der gleiche Wert heraus. Diesen Wert nennen wir in der Mathematik die Kreiszahl π (pi). Sie ist eine irrationale Zahl und hat näherungsweise den Wert 3,14.
Das könnt ihr auch leicht nachmachen. Schneidet Kreise verschiedenen Durchmessers aus und rollt sie ab, um den Umfang zu bestimmen (statt Abrollen kann man auch einen Faden nehmen). Bildet dann den Quotienten aus Umfang und Durchmesser. In Formelschreibweise sieht das dann so aus: \[ \large u = π \cdot d = 2 \cdot \pi \cdot r \] Wenn ich also den Radius oder den Durchmesser eines Kreises kenne, kann ich den Umfang berechnen und umgekehrt. Damit auch mit dem Taschenrechner nichts schief läuft, habe ich nachher noch ein paar interaktive Übungsmöglichkeiten zusammengebaut.
So, das ist nicht soooo schwer, denke ich. Da haben wir in meinen Kapiteln schon kompliziertere Dinge kennengelernt. 😉
Kommen wir nun zur
Die Herleitung ist nicht ganz so einfach. Ich möchte das mit euch im Schnellverfahren machen. Wir haben bei der Fläche von Figuren schon kannengelernt, dass das Zerschneiden sehr hilfreich sein kann. Das machen wir auch beim Kreis. Wir teilen den Kreis in gleichgroße Stücke und legen die anschließend wechselseitig zusammen.

Wir sehen, dass sich die gebildete Figur immer mehr einem Rechteck annähert, je kleiner die Stücke werden. Die Höhe der Stücke entspricht dabei dem Radius, die lange Seite entspricht dem halben Kreisumfang. Das ist logisch, da sowohl der obere als auch der untere Rand ja aus den Stücken des Kreises besteht. Die Fläche eines Rechtecks kennen wir. Es gilt: \[ \large A = a \cdot b \] Die Seite a entspricht dem halben Kreisumfang und hat daher die Länge π r. Die Seite b entspricht der Höhe der Kreisstücke und entspricht dem Radius r. Setzen wir das jetzt ein ergibt sich für die Fläche:
\[ \large A = (\pi \cdot r) \cdot r \]oder
\[ \large A = \pi \cdot r^2 \]Super! Damit haben wir die wichtigsten Dinge beim Kreis schon zusammengetragen. Wir haben u, A, r und d kennengelernt. Wir brauchen nur eines der vier Teile zu kennen, um die anderen drei auszurechnen. Hierfür habe ich euch noch ein paar Übungsmöglichkeiten zusammengestellt. Es dürfen auch Dezimalbrüche eingegeben werden. Ihr könnt die "normal" eingeben, besser aber mit "." statt ",". Die Ausgabe erfolgt wegen Javascript allerdings immer in englischer Schreibweise (also "." statt ","). Achtung! Es kann unter Umständen zu internen Rundungsfehlern kommen, so dass ihr so etwas wie 3.99999999 seht. Falls ihr die Eingabe mit "Enter" abschließt, kann es u.U. zur Anzeige einer Fehlermeldung kommen. Die dürft ihr ignorieren... Die Ergebnisse werde dennoch korrekt angezeigt.
Kommen wir nun noch zu einem Teilstück eines Kreises – sagen wir einem Tortenstück – nämlich dem
Schauen wir uns einmal einen Sektor an:
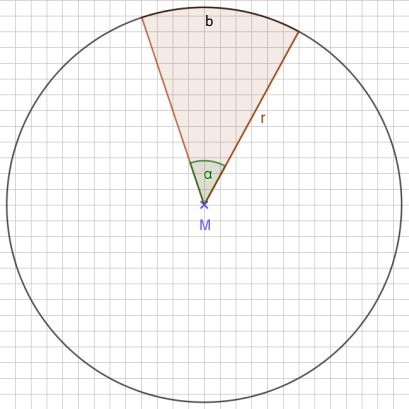
Wir sehen, das Teil ist wir ein Kuchenstück zum Mittelpunkt des Kreises herausgeschnitten. Der Umfang und die Fläche lassen sich leicht ausrechnen. Beim Umfang haben wir zunächst die beiden Seitenstücke. Die sind leicht, denn das ist der Radius des Gesamtkreises. Das obere Bogen b erfordert schon eine kleine Überlegung. Der Gesamtkreis hat einen Mittelpunktswinkel von 360° und einen Umfang von \(u = 2 \cdot \pi \cdot r \). Hier ist aber nur der Winkel α durchlaufen. Das heißt das Stück ist nur ein Bruchteil des Gesamtumfangs groß, nämlich:
\[ \large b = 2 \cdot \pi \cdot r \cdot \small \frac {\alpha}{360} \]oder gekürzt
\[ \large b = \pi \cdot r \cdot \small \frac {\alpha}{180} \]Damit ist der Gesamtumfang des Sektors
\[ \large u = 2 \cdot r + \pi \cdot r \small \cdot \frac{\alpha}{180} \]Für die Fläche eines Kreissektors gilt auch wieder, dass er ein Bruchteil der Gesamtfläche eines Kreises ist und vom Mittelpunktswinkel α abhängt:
\[ \large A = \pi \cdot r^2 \cdot \small \frac {\alpha}{360} \]So, das hätten wir geschafft. Zum Schluss noch ein paar wichtige Dinge über
Es gibt insgesamt drei Typen von Geraden am Kreis:
Eine Passante läuft am Kreis vorbei und berührt oder schneidet ihn nicht.
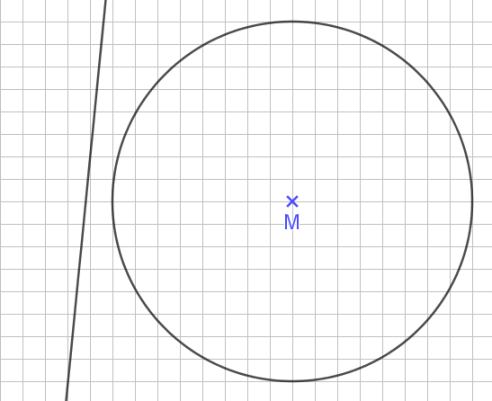
Die Sekante schneidet den Kreis in zwei Punkten
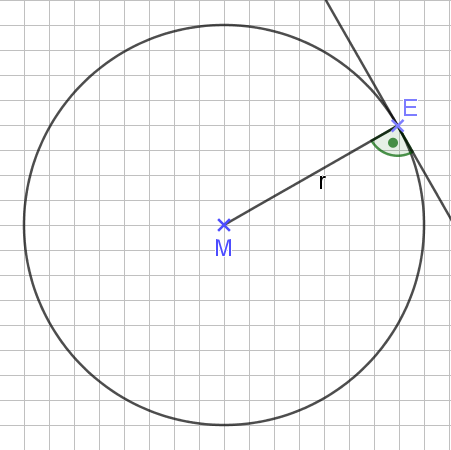
Die Tangente ist die wichtigste Linie und wird uns in späteren Betrachtungen noch weiterverfolgen.Sie berührt den Kreis in genau einem Punkt und steht senkrecht zu dem Radius durch diesen Punkt.
So, das wäre das Wichtigste über Kreise und dieses Kapitel geschafft.