
Im Gegensatz zur Figur bezeichnet man in der Geometrie 3-dimensionale Gegenstände als Körper. Körper sind also nicht eben!!!
Einfache Körper sind z.B. Würfel und Quader, der Zylinder ist etwas gesondert zu betrachten ebenso wie Spitzkörper (Pyramiden). Bei Körpern werden am häufigsten die Oberfläche und das Volumen (Rauminhalt) berechnet, weshalb ich mich hier darauf beschränke. Auch die Kugel findet hier keinen Platz, da sie etwas Besonderes ist.
Bei Körpern werden in der Regel folgende Bezeichnungen verwendet:
| Grundfläche | Das ist die Fläche, auf der der Körper steht. |
| Deckfläche | Das ist die Fläche, die den Körper oben abschließt. |
| Seitenfläche | Das sind die übrigen Flächen, die den Körper begrenzen. |
| Kante | Als Kante bezeichnet man die Linie, die sich bildet, wenn zwei Seitenflächen zusammentreffen. |
| Mantelfläche | Das ist die Summe der Flächen aller Seiten, außer der Grundfläche und der Deckfläche. |
| Oberfläche | Die Oberfläche berechnet man aus der Summe aller Flächen, die den Körper begrenzen, also Mantelfläche plus Deckflächen(n). |
| Volumen | Das Volumen ist der Rauminhalt des Körpers. |
Kommen wir zuerst zu den Prismen.
Ein Prisma ist vereinfacht geagt ein Körper, bei dem die Seitenflächen senkrecht auf der GrundflächeG stehen (für Spezialisten: den Satz von Cavalieri lassen wir jetzt mal außer Acht…) und bei dem Grundfläche und Seitenfläche im rechten Winkel zueinander stehen. Füralle diese Körper gilt für das Volumen:
\[\LARGE \boldsymbol {V = G \cdot h}\]Das ist doch schon mal eine enorme Vereinfachung. Ich muss nur wissen, wie groß die Grundfläche ist und welche Länge die Höhe hat - und fertig... Arbeiten wir uns langsam durch das Dickicht und fangen an mit dem

Der Würfel ist ein Spezialfall eines Prismas. Er ist ein Körper, der aus 6 Quadraten der Seitenlängea aufgebaut ist, die jeweils im rechten Winkel aneinandergrenzen. Daher ergeben sich bei ihm einige Vereinfachungen. Da nur Quadrate mit der Seitenlängea beteiligt sind, ergibt sich für die Grundfläche:
\[\LARGE \boldsymbol {G = a \cdot a}\]Die Höhe des Würfels ist so groß wie eine Seitenlänge, alsoh =a. Damit ergibt sich für das Volumen:
\[\LARGE \boldsymbol {V = G \cdot h}\]Damit haben wir das Volumen ferstgezurrt. Super. Kommen wir noch zur Oberfläche. Die besteht aus sechs Quadraten mit der Seitenlängea. Jedes dieser Quadrate hat die FlächeA =a². Also beträgt die Gesamtoberfläche:
\[\LARGE \boldsymbol {O = 6 \cdot a^2}\]Damit haben wir für unseren Zweck alle Teile des Würfels erledigt und kommen zum
Ein Quader ist ein Körper, der von sechs Rechtecken begrenzt wird, die jeweils im rechten Winkel zueinander stehen. Gegenüberliegende Rechtecke sind jeweils gleich. Daraus folgt aber auch, dass Grund- und Deckfläche jeweils identisch sind, auch Vorder- und Rückseite, sowie die beiden verbleibenden Seiten.

Kommen wir zunächst zum Volumen des Quaders.
Für einen Quader, der ein Rechteck mit den Seitena undb als Grundfläche hat, gilt:
Die Höhe des Quaders ist so groß wie eine Seitec, alsoh =c. Damit ergibt sich für das Volumen:
\[\LARGE \boldsymbol {V = G \cdot h}\]Für die Oberfläche des Quaders gilt ja, dass je zwei gegenüberliegende Flächen identisch sind. Also ist die Deckfläche genauso groß wie die Grundfläche, nämlich \(\boldsymbol{G = a \cdot b}\). Für die Vorderfläche gilt dann \(\boldsymbol {A = a \cdot c}\), ebenso für die Rückseite. Für die rechte Seitenfläche gilt: \(\boldsymbol {A = b \cdot c}\), ebenso für die linke. Die Gesamtoberfläche ist die Summe aller Einzelflächen, also 2x Grundfläche + 2x Vorderseite + 2x rechte Seite oder:
\[\LARGE \boldsymbol {O = 2\cdot a \cdot b + 2 \cdot a \cdot c + 2 \cdot b \cdot c}\]Damit haben wir die gängigsten Spezialfälle eines Prismas betrachtet. Kommen wir noch mal zur Ausgangsdefinition eines Prismas zurück: Ein Prisma ist ein Körper, dessen Seitenflächen Rechtecke sind, die senkrecht auf der Grundfläche stehen und Grund- und Deckfläche parallel und kongruent sind. Das heißt aber:Die Form von Grund- und Deckfläche ist dabei völlig egal! Das kann ein Dreieck sein (wie z.B. bei einer Toblerone®-Packung), ein Rechteck (Quader, Milchkarton), ein Trapez oder Parallelogramm oder... sein. Das Prisma stellt also den allgemeinsten Fall eines Körpers mit rechteckigen Seitenflächen dar. Auch hier gelten die gleichen Betrachtungen wie für Würfel und Quader. DieOberfläche ist die Summe aller Seitenflächen und dasVolumen ist gleich Grundfläche mal Höhe. Der Unterschied ist nur der, dass die Grundfläche gesondert betrachtet werden muss. Für die Berechnung des Volumens muss also zunächst geklärt werden, um welche Art von Grundfläche es sich handelt. Man hat (sinnvollerweise!) festgelegt, dass die rechteckigen Flächen immer die Seitenflächen sind. Die verbleibenden Flächen sind Grund- und Deckfläche.
Spielen wir das Ganze einmal am folgenden Beispiel durch, nämlich dem:
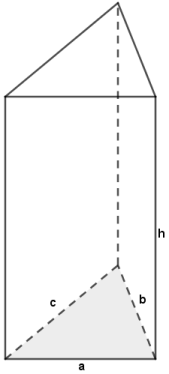
Das Prisma hat die Grundfläche mit den Seitena,b undc. Daran ändert sich auch nichts, wenn das Prisma auf der Seite liegt (s. folgende Abbildung: die graue Fläche ist bei beiden Prismen die Grundfläche)
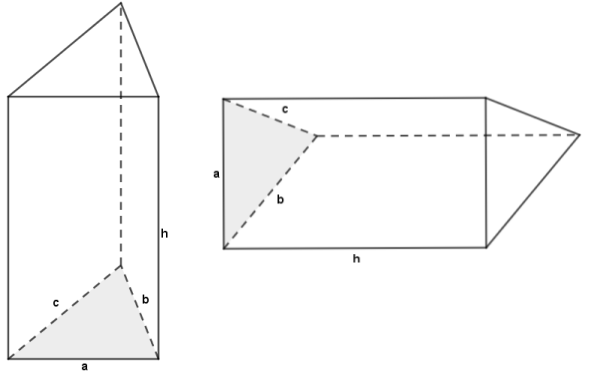
Also, die Grundfläche wird aus einem Dreieck mit den Seitena,b undc gebildet. Darauf steht jeweils ein Rechteck mit der Höheh. Für das Volumen gilt ja:
\[\LARGE \boldsymbol {V = G \cdot h}\]Da die Grundfläche ein Dreieck ist, gilt, wenn wir die Seitea zu Grunde legen:
\[\LARGE \boldsymbol {G = {{a \cdot h_a} \over 2}}\]Entsprechend kann ich natürlich auch die Seiteb oderc der Grundläche nehmen.
Für die Oberfläche gilt dann, dass zweimal die Grundfläche und die Fläche aller Seitenrechtecke addiert werden müssen. Beim Dreiecksprisma ergibt das:
So, nun haben wir das ausführlich bei einer nicht-rechteckigen Grundfläche betrachtet. Für ein Parallelogramm, Trapez, Sechseck... als Grundfläche müssen wir also dann die entsprechenden Formeln für die Grundfläche benutzen. Also ist das auch wieder nichts wirklich Neues 😊. Damit sollten die Probleme mit der Berechnung von Oberfläche und Volumen eines Prismas der Vergangenheit angehören.
Kommen wir zu noch einem Spezialfall, nämlich dem:
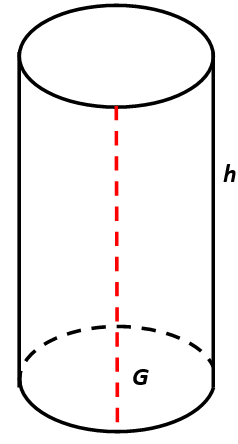
Für das Volumen gilt ganz normal: \(V = G \cdot h\). Wie wir gerade gelernt haben, kommt es nun auf die Grundfläche an. Die ist ein Kreis. Daher gilt für den Flächeninhalt der Grundfläche:
\[\LARGE \boldsymbol {G = \pi \cdot r^2}\]Damit haben wir alles für das Volumen des Zylinders. Es beträgt:
\[\LARGE \boldsymbol {V = \pi \cdot r^2 \cdot h}\]Um die Oberfläche des Zylinders zu bestimmen brauche ich neben der Grund- und Deckfläche auch die Mantelfläche. Und die ist das eigentliche schwierigere Problem, da es ja keine Kanten gibt, die zusammentreffen.
Hmmm... überlegen wir, wie wir da rankommen:
Die Mantelfläche umschließt ja komplett den Kreis der Grundfläche. Trennt man sie an der gestrichelten, roten Linie auf und rollt sie ab, erhält man ein Rechteck dessen eine Seite die Länge von h hat. Die andere Seite hat den Kreis der Grundfläche umschlossen, ist also genauso lang wie der Umfang des Kreises, nämlich \(u = 2 \cdot \pi \cdot r\). Damit gilt für die Fläche des Mantels:
Für die gesamte Oberfläche muss ich Grundfläche, Deckfläche und Mantelfläche addieren. Grund- und Deckfläche sind gleich. Daraus ergibt sich:
\[\LARGE \boldsymbol {O = 2 \cdot \pi \cdot r^2 + 2 \cdot \pi \cdot r \cdot h}\]So, nun haben wir wirklich alle relevanten Spezialfälle bei den Prismen durchgespielt. Ich hoffe, es bleiben da keine Wünsche offen. Was noch bleibt, sind die
Die behandele ich an dieser Stelle nur ganz kurz. Da können wir nämlich viele Dinge mit machen und anwenden, wie z.B. den Satz des Pythagoras, trigonometrische Funktionen und, und, und... Daher an dieser Stelle nur das Notwendigste.
Wodurch zeichnen sich Pyramiden aus? Sie haben als Grundfläche ein n-eck, aber keine Deckfläche. Die Kanten der Seitenflächen laufen in einem geminsamen Punkt zusammen, der (zunächst der Einfachheit halber) senkrecht über dem Mittelpunkt der Grundfläche liegt (Für Spezialisten: auch hier lassen wir den Satz von Cavalieri außer Acht). Das klassische Beispiel dafür sind die Pyramiden aus Ägypten. Da die Kanten der Seitenflächen oben in einem Punkt, der Spitze, zusammenlaufen, sind alle Seitenflächen Dreiecke. Das unterscheidet die Pyramiden deutlich von den Prismen. Die Form des n-ecks ist wiederum komplett egal. Es kann ein Quadrat sein (wie bei dem klassischen Pyramiden), aber auch ein 5-eck, Trapez oder was auch immer. Haben wir denn dann auch kompliziertere Berechnungen beim Volumen und der Oberfläche? Zum Glück: Nein! Während beim Prisma das Volumen Grundfläche mal Höhe ist, ist bei den Pyramiden das nur ein Drittel davon oder
Die übrigen Überlegungen sind so, wie beim Prisma. Mehr ist das nicht. Für die Oberfläche gilt auch hier: ich addiere die Grundfläche und alle Seitenflächen (eine Deckfläche gibt es ja nicht). Die Seitenflächen sind aber alles Dreiecke. hier muss ich also sehen, wo ich die entsprechenden Höhen herbekomme, denn ohne die geht leider gar nichts, wie wir bei der Flächenberechnung von Dreiecken ja schon gehört haben. Aber das spielen wir in einem Extrakapitel durch. Natürlich gibt es auch hier noch einen Spezialfall, nämlich den:
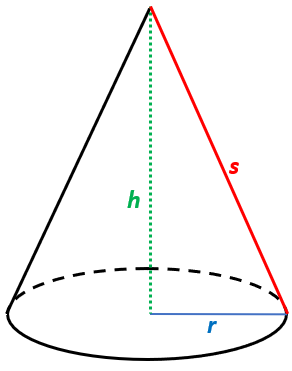
Wie bei seinem Pendant bei den Prismen (Zylinder) ist das Volumen das geringste Problem. Die Grundfläche ist ein Kreis, also ist die Grundfläche \(G = \pi \cdot r^2\). Und da er ein Spitzkörper ist, ist dass Volumen nur \({1 \over 3}\) mal so hoch, wie beim Zylinder. Also gilt für das Volumen:
\[\LARGE \boldsymbol {V = {1 \over 3} \cdot \pi \cdot r^2 \cdot h}\]Okay, also alles ganz normal. Für die Oberfläche brauche ich aber noch die Mantelfläche. Das ist - wie beim Zylinder - auch hier der springende Punkt. Wie kommen wir dahin? Das ist leider nicht so ganz einfach, wie beim Zylinder. Ich brauche unbedingt die kürzeste Entfernungs von der Spitze bis zur Kreislinie. Entweder ist die gegeben, okay, leichtes Spiel, oder ich muss sie mit dem Pythagoras bestimmen. Wenns gegeben ist gilt für die Mantelfläche:
\[\LARGE \boldsymbol {M = \pi \cdot r \cdot s}\]und damit für die Oberfläche:
\[\LARGE \boldsymbol {O = G + M}\]So, das war's in Kürze zu den Pyramiden. Im Prinzip ist alles ähnlich wie bei den Prismen, nur dass die Seitenflächen hier Dreiecke sind.
Zuletzt noch die große Frage: Wozu braucht man das???? Nun, alle, die mit Werkstücken zu tun haben, kommen früher oder später damit in Berührung, wenn es um Masse und Rohstoffverbrauch geht. In der Praxis hat man es allerdings kaum mit einfachen Körpern zu tun, die man einfach berechnen kann. In der Regel handelt es sich um zusammengesetzte Körper. Diese muss man geschickt zerlegen und dann die erhaltenen Einzelkörper berechnen. Nehmen wir folgendes Werkstück:
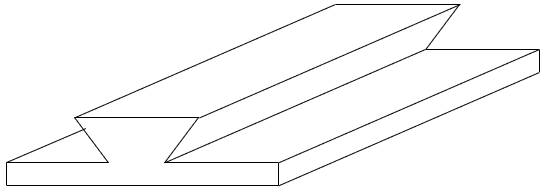
Dieses Werkstück hier, können wir z.B. in zwei Teile zerlegen, nämlich einen Quader und ein Prisma mit trapezförmiger Grundfläche:
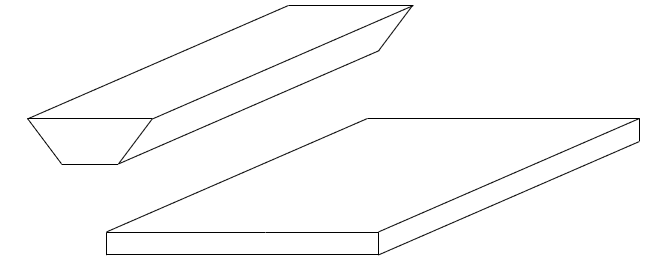
Beide Teilkörper können dann getrennt berechnet werden. Beim Volumen muss also das Volumen des Quaders und das des Prismas bestimmt werden. Das Gesamtvolumen ist dann die Summe der beiden Einzelvolumina:
\[\LARGE \boldsymbol {V = V_{Prisma} + V_{Quader}}\]Das war jetzt mal nur ein kleiner Ausflug in die Realität, denn Mathematik ist bei weitem nicht Selbstzweck sondern erleichtert uns in Alltag und Beruf doch eine ganze Menge. Das sollten wir immer im Auge behalten, auch wenn ein Teilkapitel mal nicht gerade den großen Spaßfaktor hat.