Bei Gleichungssystemen geht es immer um folgenden Sachverhalt: man will herausfinden, wo zwei Funktionen diegleichen Werte haben, das heißt der x-Wertund der y-Wert sind jeweils gleich. Anders ausgedrückt: wir suchen den Schnittpunkt zweier Funktionen. Um diese Werte zu bestimmen, gibt es mehrere Verfahren. Welches wir letztendlich benutzen, bleibt uns selbst (oder dem Mathelehrer 😉) überlassen. Alle Verfahren liefern am Ende das gleiche Ergebnis!
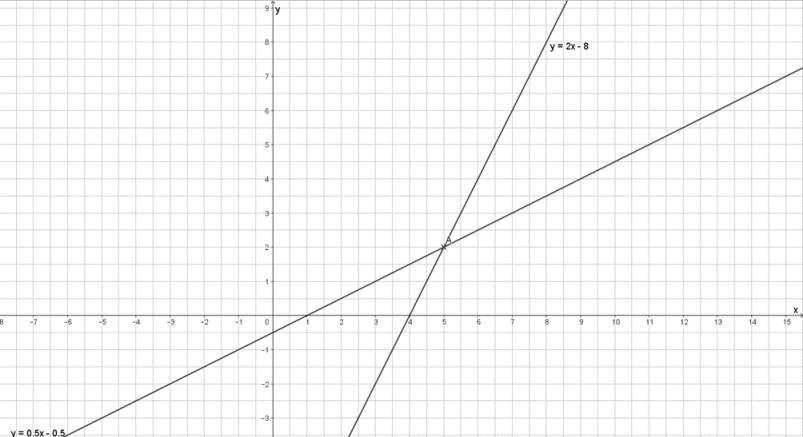
Graphisch geht das ganz einfach. Man zeichnet das Schaubild beider Funktionen gemeinsam in ein Koordinatensystem und liest den Schnittpunkt ab. Beispiel:
Gegeben sind die Funktionen
\begin{align} \text{I:}~~y &= 2x - 8~\text{und} \\ \text{II:}~~y &= 0,5x - 0.5\end{align}

Wir sehen, die beiden Geraden schneiden sich bei S (5 | 2). Also ist das die Lösung des Gleichungssystems.
Das kann man aber auch ganz elegant mit Geogebra machen. Wir geben in der Eingabezeile nacheinander die beiden Funktionsgleichungen ein und bestätigen mit ENTER. Danach wählen wir das Schnittpunkwerkzeug aus dem Punktmenü aus. Das heißt hier: Schneide.
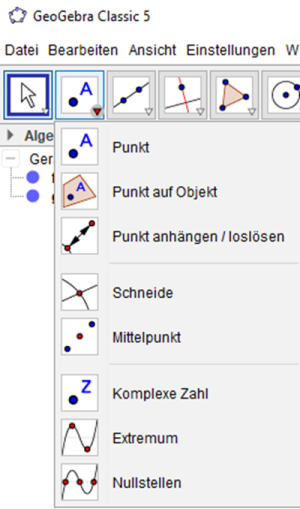
Danach klicken wir im Algebrafenster nacheinander auf die beiden Funktionsgleichungen und erhalten sofort die Koordinaten des Schnittpunktes.
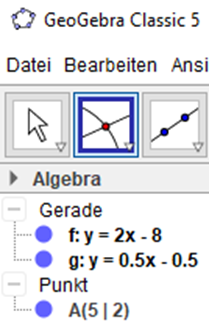
Das klappt immer! Das ist besonders praktisch, wenn die beiden Funktionen sich erst bei sehr hohen Werten schneiden. Aber auch bei niedrigen Werten erleichtert es die Arbeit. Natürlich könnt ihr Geogebra auch hernehmen und schauen, ob ihr mit den anderen Verfahren, die jetzt folgen, richtig gerechnet habt. Ihr habt dann immer die Kontrolle.
Kommen wir nun zum ersten rechnerischen Verfahren, dem
Das Gleichsetzungsverfahren benutzt man dann, wenn auf einer Seite bei beiden Funktionsgleichungen derselbe Ausdruck für eine Unbekannte steht. Beispiel:
Gegeben sind die Funktionen
\begin{align} \text{I:}~~3x &= -3y - 3~\text{und} \\ \text{II:}~~3x &= -y + 3\end{align}
Hinweis: Manchmal stehen die Gleichungen nicht in der Form, wie wir sie brauchen, dann müssen wir sie vorher „in Form“ bringen, z.B. durch Termumformungen.Auf der linken Seite steht jetzt jeweils: \(3x\).
Da wir den Schnittpunkt der beiden Funktionen suchen wissen wir, dass die x-Werte gleich sein müssen. Daher muss für beide Funktionen auch \(3x\) gleich sein. Wenn die linke Seite beider Funktionen am Schnittpunkt gleich ist, muss aber auch die rechte Seite beider Funktionen am Schnittpunkt gleich sein. Daher dürfen wir schreiben:
Diese Gleichung lösen wir nun nach y auf:
\begin{align} -3y - 3 &= -y + 3 ~~~|+3y\\ -3 &= 2y + 3 ~~~~|-3\\ -6 &= 2y ~~~~~~~~~~|:2\\ -3 &= y\end{align}Jetzt habe ich den y-Wert ausgerechnet, bei dem sich die Funktionen schneiden. Nun muss ich als nächstes den x-Wert ausrechnen, bei dem der Schnittpunkt liegt. Das bedeutet, ich muss in einer der beiden Ausgangsgleichungen den gefundenen Wert für y einsetzen. Dann erhalte ich den x-Wert. Welche der beiden Ausgangsfunktionen ich nehme ist völlig egal, da ja (wegen der Schnittpunktsuche) derselbe Wert herauskommen muss. In unserem Beispiel setze ich den Wert in Funktion I ein:
\[3x = -3y - 3\]Jetzt ersetze ich in dieser Funktion y durch den gefunden Wert (Achtung! -3y heißt: -3 mal y):
\[3x = -3 \cdot (-3) - 3\]Nun rechne ich erst aus
\[3x = 9 - 3\]fasse zusammen und löse auf
\begin{align} 3x &= 6 ~~~~~~|:3\\ x&= 2 \end{align}Nunmehr habe ich sowohl die x-Koordinate als auch die y-Koordinate des Schnittpunkts. Er liegt bei S (2 |-3).
Habe ich bei den Variablen unterschiedliche Vorzeichen, empfiehlt sich häufig das
Das Additionsverfahren benutzt man dann, wenn auf einer Seite bei beiden Funktionsgleichungen derselbe Ausdruck für eine Unbekannte einmal mit positivem und einmal mit negativem Vorzeichen steht. Beispiel:
Gegeben sind die Funktionen
\begin{align} \text{I:}~~7x + 4y &= 9~\text{und} \\ \text{II:}~~x - 4y &= 79\end{align}
Wenn ich jetzt beide Gleichungen addiere, fällt der Term für y weg (Achtung!!!! Schreibe die beiden Funktionsgleichungen immer so untereinander, dass Gleichheitszeichen unter Gleichheitszeichen steht.). Dann kann ich den x-Wert problemlos ausrechnen. Also:
\[7x + 4y = 9\] \[\underline{~~~~~x - 4y = 79}\] \[~~~~~~~~~~8x = 88\]Jetzt löse ich normal auf:
\begin{align} 8x &= 88 ~~~~~|∶8\\ x &= 11 \end{align}Jetzt habe ich den x-Wert ausgerechnet, bei dem sich die Funktionen schneiden. Nun muss ich als nächstes den y-Wert ausrechnen, bei dem der Schnittpunkt liegt. Das bedeutet, ich muss in einer der beiden Ausgangsgleichungen den gefundenen Wert für x einsetzen. Dann erhalte ich den y-Wert. Welche der beiden Ausgangsfunktionen ich nehme ist völlig egal, da ja (wegen der Schnittpunktsuche) derselbe Wert herauskommen muss. In unserem Beispiel setze ich den Wert in Funktion I ein:
\[7x + 4y = 9\]Jetzt ersetze ich in dieser Funktion x durch den gefunden Wert (Achtung! 7x heißt: 7 mal x):
\[7 \cdot 11 + 4y = 9\]Nun rechne ich erst aus
\[77 + 4y = 9\]und fasse zusammen
\begin{align} 77 + 4y &= 9~~~~~~~~~~~~~|-77\\ 4y &= -68 ~~~~~~~~|∶4\\ y &= -17 \end{align}Nunmehr habe ich sowohl die x-Koordinate als auch die y-Koordinate des Schnittpunkts. Er liegt bei S (11 |-17).
Letztendlich ist es vollkommen egal, welches der Verfahren ich zur Lösung eines Gleichungssystems verwende. Es muss immer die gleiche Lösung herauskommen. Ich habe euch hier die gängigsten Verfahren in Reinform vorgestellt. Wie ich beim Gleichsetzungsverfahren schon angedeutet habe, muss man, wenn der Mathelehrer es so möchte, Gleichungen umstellen, um mit dem entsprechenden Verfahren arbeiten zu können. Das ändert aber nichts an den Verfahren selbst und auch nichts am Verständnis, wie ich so ein Problem lösen kann. Und zu guter letzt habt ihr ja noch Geogebra, um eure schriftlichen Verfahren - zumindest zu Hause - überprüfen zu können. 😉