Wie zeichne ich eine Gerade, wenn ich einen Punkt und die Steigung kenne?

Wir wissen: Ich brauche genau zwei Punkte, um eine Gerade eindeutig zeichnen zu können.

Okay, die Punkte muss ich irgendwoher bekommen. Schauen wir, wie wir das hinkriegen. Das ist auch nicht wirklich schwer. Folgende Bedienungsanleitung sollte euch helfen, eine Gerade problemlos zu zeichnen. Die einzelnen Schritte sind:

  1. Die Geradengleichungmuss in der Form \(y = mx + b\) vorliegen, wenn nicht, muss ich sie entsprechend umstellen.

  2. \(b\) gibt immer den Schnittpunkt mit der \(y\)-Achse an. Das ist mein erster Punkt der Geraden.

  3. Ich schreibe die Steigung (das ist der Faktor vor dem \(x\))immer als Bruch.

  4. Ich gehe dann zum Schnittpunkt der Geraden mit der \(y\)-Achse. Von dort gehe ich um so viele Einheiten nach rechts (parallele zur \(x\)-Achse), wie imNenner der Steigung steht und markiere mir einen kleinen Hilfspunkt.

Beispiele

A       \(\boldsymbol{y = 2x - 4}\)

  1. Die Geradengleichung liegt schon in der richtigen Form vor.

  2. \(b\) ist – 4. Also wird die \(y\)-Achse bei – 4 geschnitten. Ich markiere den Punkt.

  3. Die Steigung ist 2. Also schreibe ich \({2 \over 1}\).

  4. Vom Schnittpunkt der Geraden mit der \(y\)-Achse aus gehe ich nun eine Einheit (Nenner ist 1) nach rechts und zwei Einheiten (Zähler ist 2) nach oben (die Steigung ist positiv). Dort erhalte ich den zweiten Punkt der Geraden und kann die Gerade mit dem Lineal zeichnen.

B       \(\boldsymbol {y = -{3 \over 4}x + 2}\)

  1. Die Geradengleichung liegt schon in der richtigen Form vor.

  2. \(b\) ist + 2. Also wird die \(y\)\(y\)-Achse bei 2 geschnitten. Ich markiere den Punkt.

  3. Die Steigung ist \(-{3 \over 4}\).

  4. Vom Schnittpunkt der Geraden mit der \(y\)-Achse aus gehe ich nun vier Einheiten (Nenner ist 4) nach rechts und drei Einheiten (Zähler ist 3) nach unten (die Steigung ist negativ). Dort erhalte ich den zweiten Punkt der Geraden und kann die Gerade mit dem Lineal zeichnen.

C       \(\boldsymbol {8x - 2y = 2}\)

  1. Die Geradengleichung liegt nicht in der richtigen Form vor. Ich muss umformen.
    \begin{align} 8x - 2y &= 2 ~~~~~~~~~~~~~~| + 2y\\ 8x &= 2 + 2y ~~~~~|  - 2\\ 8x -2 &= 2y ~~~~~~~~~~~~|  ∶ 2\\ 4x - 1 &= y \end{align} Die Geradengleichung lautet also in der gewohnten Schreibweise: \[\boldsymbol {y = 4x - 1}\] Jetzt liegt die Geradengleichung in der passenden Form vor und ich kann weiterarbeiten.
  2. \(b\) ist – 1. Also wird die \(y\)-Achse bei – 1 geschnitten. Ich markiere den Punkt.

  3. Die Steigung ist 4. Also schreibe ich \(4 \over 1\).

  4. Vom Schnittpunkt der Geraden mit der \(y\)-Achse aus gehe ich nun eine Einheit (Nenner ist 1) nach rechts und vier Einheiten (Zähler ist 4) nach oben (die Steigung ist positiv). Dort erhalte ich den zweiten Punkt der Geraden und kann die Gerade mit dem Lineal zeichnen.

Die gerade beschriebenen Beispiele habe ich noch als Bild beigefügt:

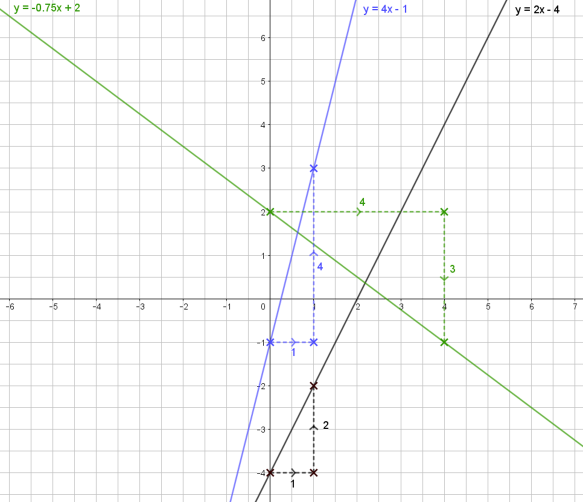
Koerper_6

Wenn wir das Ganze noch mal Revue passieren lassen, ist das wirklich nicht schwer. Wir müssen im Grunde genommen noch nicht einmal richtig verstanden haben, was da passiert. Wir müssen nur die Anleitung Schritt für Schritt durchgehen und bekommen ein tolles Ergebnis. So soll es sein. Und die Spezialisten können hier eh noch weitere Dinge sehen. 😉

Für Leute, die nicht sicher mit dem Umrechnen der Geradengleichung sind: Geogebra kann euch dabei helfen. Ihr tippt die Geradengleichung so wie sie ist in die Eingabezeile und bestätigt mit <Enter>. Je nach Voreinstellung seht ihr im Algebrafenster schon die umgeformte Gleichung. Wenn nicht, mit der rechen Maustaste auf die Gleichung im Algebrafenster klicken und dann im aufgehenden Menüy = mx + t wählen (Linksklick). Schon seht ihr die Geradengleichung in der passenden Form.