Wie du die Fläche eines Rechtecks bestimmts, hast du schon gelernt:
\[\Large \boldsymbol {A = {{a \cdot b}}}\]Auch die Fläche eines Quadrats (für Spezialisten: als Sonderfall des Rechtecks) kannst Du schon bestimmen:
\[\Large \boldsymbol {A = {{a \cdot a}}= a^2}\]Wie sieht das nun bei den anderen speziellen Vierecken aus? Wir werden sehen: gar nicht so schwer. Was brauchen wir?
Also, das scheint nicht soooo schwer zu werden, das kriegen wir hin!!
Bei einem Parallelogramm kann man durch B oder D eine Senkrechte zur gegenüberliegenden Seite errichten. Dadurch wird ein kleines Dreieck abgeschnitten.

Dieses Dreieck schneiden wir ab und legen es an der anderen Seite wieder dran.
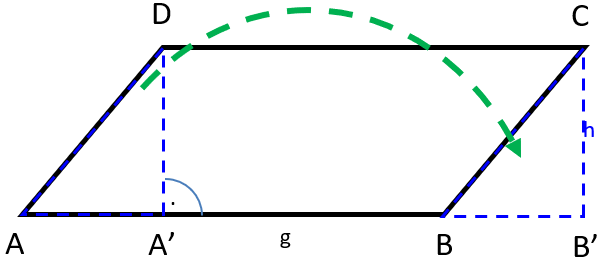
Und was passiert? Wir erhalten ein Rechteck mit den Eckpunkten A‘, B‘, C und D. Hilft uns das? Klar! Wir wissen, die StreckeAA' ist genauso lang wie die Strecke BB'.Wir haben ja nur das kleine Dreieck AA‘D nach rechts geschoben. Es wurde zum Dreieck BB’C. Damit ist die Strecke AB genauso lang wie die Strecke A'B'. Damit können wir den Flächeninhalt des Rechtecks ausrechnen, da wir die Seite g und die Seite h kennen. Also gilt für den Flächeninhalt eines Parallelogramms:
\[\Large \boldsymbol {A = {{g \cdot h}}}\]Natürlich kann man das Parallelogramm auch um 90° drehen und dann schneiden. Deswegen bleibt der Flächeninhalt aber gleich. Deswegen kann (und sollte man) besser formulieren:
Die Fläche eines Parallelogramms berechnet man aus dem Produkt einer Seitenlänge mit der Länge der Höhe (=Senkrechte) auf dieser Seite.
oder
\[\Large \boldsymbol {A = {{b \cdot h_b}}}\]Super. Das lief doch! Und weiter geht's:
Wieso kommen jetzt Dreiecke? Ganz einfach, wir haben gerade etwas gelernt, das wir prima gebrauchen können. Zwei identische Dreiecke kann man nämlich immer zu einem Parallelogramm ergänzen.
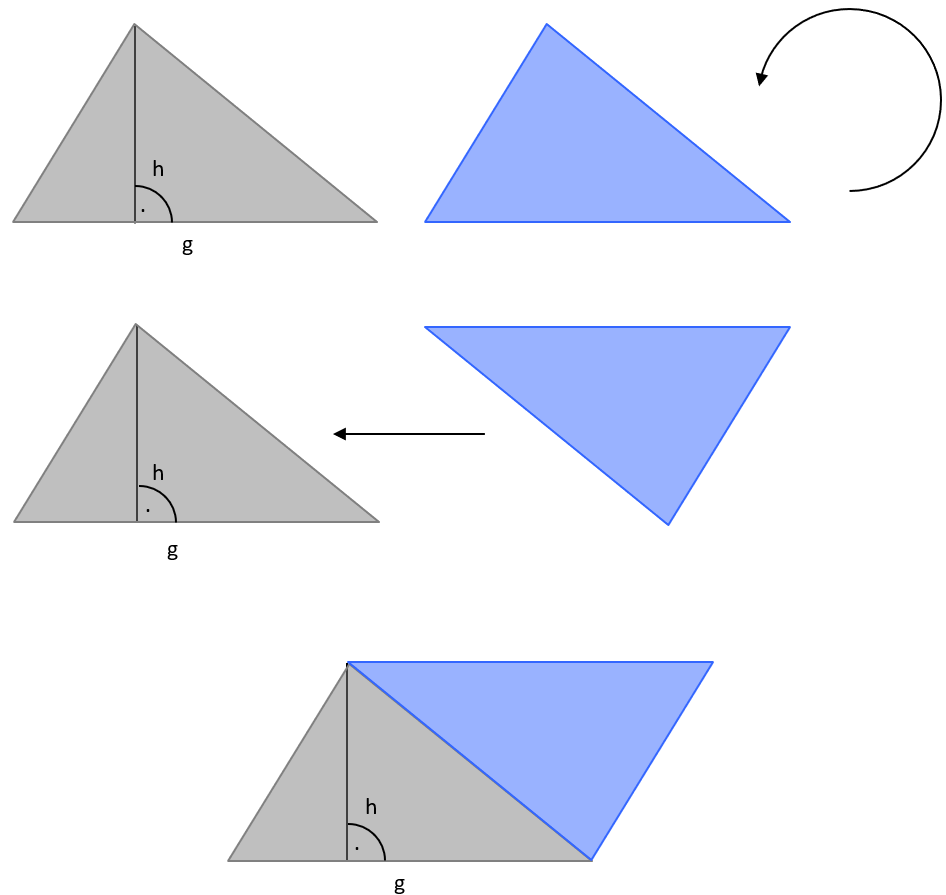
Das entstehende Parallelogramm ist doppelt so groß wie das ursprüngliche Dreieck, es hat dieselbe Höhe und dieselbe Grundseite. Also ist der Flächeninhalt des Dreiecks halb so groß wie der des entstandenen Parallelogramms:
\[\Large \boldsymbol {A = {{g \cdot h} \over 2}}\]Also ist das tatsächlich nicht etwas grundlegend Neues. Wir haben nur das benutzt, was wir schon kennen. Und damit sind wir eigentlich schon mitten in der höheren Mathematik. Der Mathematiker versucht nämlich, ein Problem mit bereits bekannten Mitteln und Methoden zu lösen. Das ist zugegebenermaßen nicht immer so ganz leicht, aber diese Probleme bewegen sich auch auf einer viel abstrakteren Ebene. Aber das Grundprinzip ist genau das, was wir hier gemacht haben.
Wir können die beiden Dreiecke mit beiden Seiten a oder b oder c aneinanderlegen, um ein Parallelogramm zu erhalten. Das kann man mit zwei ausgeschnittenen Dreiecken gut probieren. Alle drei Parallelogramme haben natürlich die gleiche Fläche, was auch einleuchtet, denn schließlich werden die Dreiecke ja nicht verändert, sondern nur anders zusammengeschoben. Deshalb kann (und sollte) man sagen:
Die Fläche eines Dreiecks berechnet man aus dem Produkt der Hälfte einer Seitenlänge mit der Länge der Höhe auf dieser Seite.
\[{\Large \boldsymbol A = {{\color{indianred} {\boldsymbol c \cdot \boldsymbol h_\boldsymbol c}} \over \boldsymbol 2}}\]
oder
\[{\Large \boldsymbol A = {{\color{dodgerblue} {\boldsymbol b \cdot \boldsymbol h_\boldsymbol b}} \over \boldsymbol 2}}\]oder
\[{\Large \boldsymbol A = {{\color{red} {\boldsymbol a \cdot \boldsymbol h_\boldsymbol a}} \over \boldsymbol 2}}\]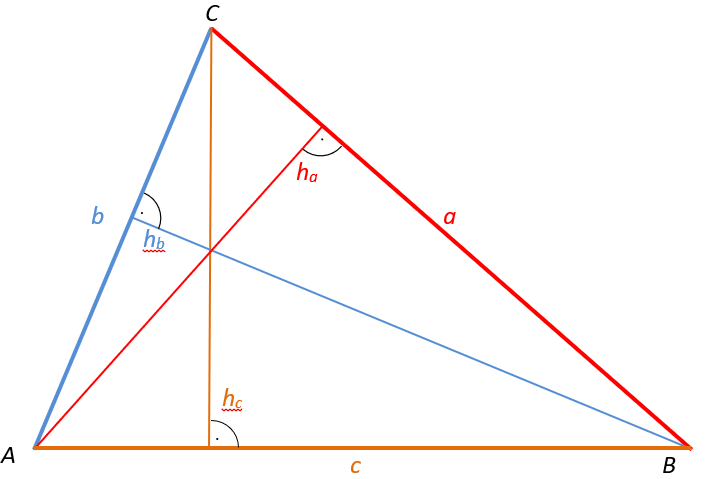
Jetzt wissen wir, dass wir Flächeninhalte mit Zerschneiden erhalten können. Das machen wir auch beim Trapez so. Wir nehmen uns auch gleich ein schiefes Trapez vor, nicht dass da einer meint, das geht nur bei symmetrischen Trapezen 😉.
Dazu zeichnen wir die Mittelparallele m ein. Vom Schnittpunkt der Mittelparallelen mit den bei-den Schenkeln des Trapezes zeichnen wir eine Senkrechte zur Seite a. Die beiden entstehenden Dreiecke werden wieder abgetrennt und jeweils oben angesetzt.
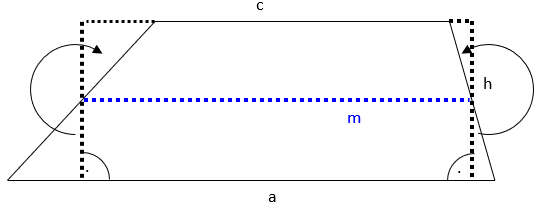
Auch hier ergibt sich wieder ein Rechteck, das dieselbe Höhe hat, wie das ursprüngliche Trapez. Die Grundseite des Rechtecks ist genauso lang, wie die Mittelparallele im Trapez. Damit ergibt sich als Fläche:
\[\Large \boldsymbol {A = {{m \cdot~ h}}}\]Die Länge der Mittelparallelen ist allerdings häufig schlecht zugänglich. Es gilt aber, dass die Länge der Mittelparallelen halb so groß ist wie die Summe der Längen der beiden Parallelen. Oder:
\[\Large m = {{a + c} \over 2}.\]
Damit gilt dann für die Fläche eines Trapezes:
\[\LARGE \boldsymbol {A = {{a + c} \over 2} \cdot h}\]
War doch gar nicht so schlecht – oder?
Was fehlt uns noch? Genau, der Drache...
Schauen wir uns einen Drachen einmal genauer an:
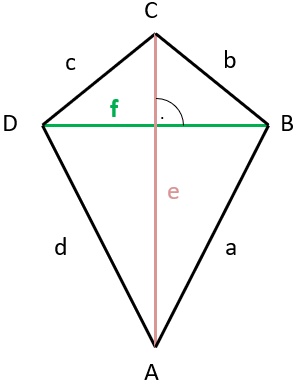
Wir sehen, das sind doch eigentlich zwei gleiche Dreiecke, die zusammengelegt wurden. Kann man da nicht etwas machen? Okay, trennen wir den Drachen entlang der Linie AC auf:
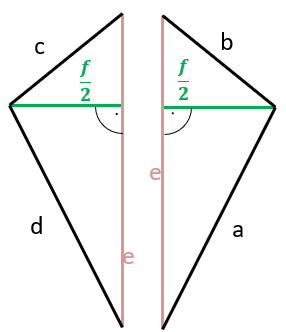
Wir erhalten zwei identische Dreiecke. Den Flächeninhalt eines Dreiecks können wir ja jetzt berechnen. Das haben wir gerade gelernt. Wir kennen die Seitee und darauf steht die Seitef senkrecht. Wenn ich beide Längen kenne, ergibt sich als Fläche eines Dreiecks:
\[\Large \boldsymbol {A = {\color{indianred} e \cdot {\color{LimeGreen} f \over \color{LimeGreen} 2} \over 2}}\]Beide erhaltenen Dreiecke sind identisch. Also ist der Flächeninhalt des Drachens so groß, wie das beider Dreiecke zusammen. Also addieren wir einfach:
\[\large \boldsymbol {A_{gesamt} = {\color{indianred} e \cdot {\color{LimeGreen} f \over \color{LimeGreen} 2} \over 2} + {\color{indianred} e \cdot {\color{LimeGreen} f \over \color{LimeGreen} 2} \over 2} = {\color{indianred} e \cdot {\color{LimeGreen} f \over \color{LimeGreen} 2} }}\]oder
\[\large \boldsymbol {A = {1 \over 2} \cdot {\color{indianred} e \cdot {\color{LimeGreen} f} }}\]Das heißt: wir können ganz einfach den Flächeninhalt eines Drachen bestimmen, wenn wir die Länge seiner beiden Diagonalene undf kennen.
Und wieder haben wir nicht wirklich etwas Neues gemacht! Super! Nur gewusst wie – und Mathe ist gar nicht so schwer 😊