Es gibt mehrere Formeln, wie man die Fläche eines regelmäßigen n-Ecks ausrechnen kann. Viele sind mehr oder weniger (meistens mehr!) kompliziert. Ich baue hier auf ein Verfahren, dass nur Dinge benutzt, die wir schon einmal kennengelernt haben und die wir (hoffentlich!) nachvollziehen können.
Das ist ja nicht viel. Dann kriegen wir das hin:
Regelmäßige n-Ecke sind aus n gleichschenkligen Dreiecken aufgebaut. Wenn ich Fläche eines dieser Dreiecke ausrechnen kann, kenne ich die Fläche des gesamten Vielecks, die ist nämlich n-mal so groß. Also ran:
Der Winkel \(\alpha\) des Dreiecks im Mittelpunkt des n-ecks lässt sich leicht berechnen. Wenn ich alle n Dreiecke zum n-Eck zusammenlege ist die Summe 360°. Das heißt auf ein Dreieck fällt der n-te Teil also \(~\alpha = {360° \over n}\).
Zu kompliziert? Okay, machen wir das an einem Beispiel: Ein regelmäßiges Fünfeck besteht aus fünf gleichschenkligen Dreiecken.
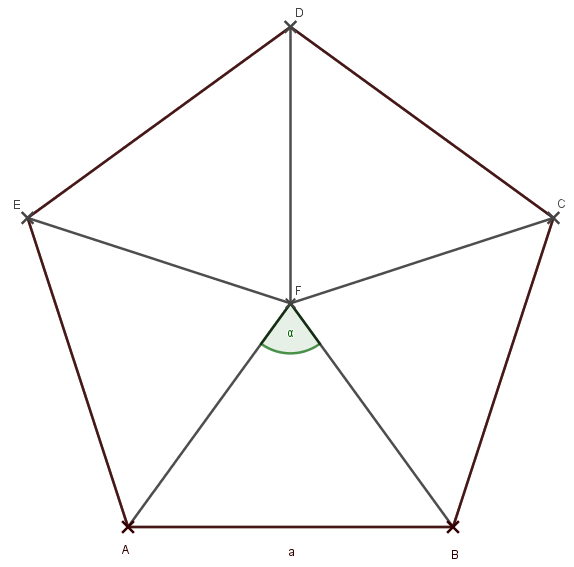
Alle fünf Dreieckswinkel in F sind gleich groß und damit: \(~\alpha = {360° \over 5} = 72°\). Das ist doch schon gleich überschaubarer…
Wir wollen nun die Fläche des Dreiecks ABF bestimmen. Daher zeichnen wir die Höhe \({\color{red}h}\) auf a ein. Diese teilt den Winkel α in F in zwei Teile zu je \(~{\alpha \over 2} = 36°\) und halbiert die Seite a.
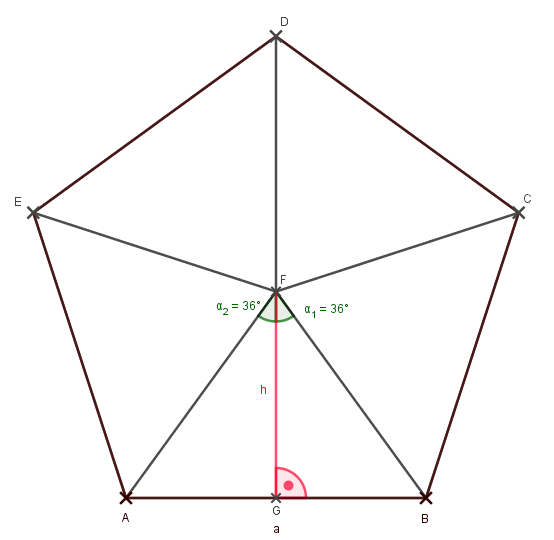
Damit erhalte ich ein rechtwinkliges Dreieck GBF. Die Länge der Strecke (hier: Gegenkathete) kenne ich. Sie ist nämlich die Hälfte von a. Ich kenne auch den Winkel \(~{\alpha \over 2}\). Damit kann ich die Höhe des Dreiecks ABF mit Hilfe des Tangens ausrechnen, denn die Höhe \({\color{red}h}\) (hier: Ankathete) brauche ich, um die Fläche des Dreiecks ABF zu bestimmen. Wir erinnern uns:
\[tan~ \alpha = {Gegenkathete \over Ankathete}\]Konkret:
\[tan~ {\alpha \over 2} = {{a \over 2} \over {\color{red}h}}\]umgeformt (Doppelbruch!):
\[\color{red}{h = {a \over 2~tan{\alpha \over 2}}}\]Super! Jetzt habe ich die Länge der Höhe im Dreieck \(ABF~\)!
Die Fläche dieses Dreiecks beträgt ja:
Okay…. Die Länge der Seite a kenne ich, die Länge der Höhe h haben wir gerade ausgerechnet. Also setzen wir den Term für h ein:
\[A = {a \over 2} \cdot \color{red}{a \over 2~tan{\alpha \over 2}}\]umgeformt:
\[A = {a^2 \over 4~ tan {\alpha \over 2}}\]Nun haben wir die Flächeeines Dreiecks ausgerechnet. Das gesamte n-eck besteht aber aus n solcher Dreiecke. Also müssen wir das Ergebnis noch mit n multiplizieren:
\[\large \boldsymbol{A = {n \cdot a^2 \over 4~ tan {\alpha \over 2}}}\]Fertig. Huch! Damit haben wir sogar die Formel bestimmt, die Fläche eines beliebigen, regelmäßigen n-ecks auszurechnen. 😊 Kompliziert? Nööö…
Also: schnell zurück zu unserem regelmäßigen Fünfeck für das a= 6 cm betragen soll:
Hmmmm…, was brauchen wir?
Anzahl der Ecken: 5
Seitenlänge: 6
Winkel im Mittelpunkt des 5-ecks: \(\alpha = \color{#00B050}{72}° (\alpha = {360° \over 5})\)
Dementsprechend hat dieses regelmäßige Fünfeck eine Fläche von:
\[A = {\boldsymbol{\color{#C45911}5 \cdot \color{#00B0F0}6}^2 \over 4~ tan {\color{#00B050}{72} \over 2}}\] \[ \Large \boldsymbol{A = 61,94~cm^2}\]Klasse! Versuchen wir das doch gleich nochmal bei einem regelmäßigen 6-eck mit a = 7 cm.
Was brauchen wir?
Anzahl der Ecken: 6
Seitenlänge: 7
Winkel im Mittelpunkt des 5-ecks: \(\alpha = \color{#00B050}{60}° (\alpha = {360° \over 6})\)
Dementsprechend hat dieses regelmäßige Fünfeck eine Fläche von:
\[A = {\boldsymbol{\color{#C45911}6 \cdot \color{#00B0F0}7}^2 \over 4~ tan {\color{#00B050}{60} \over 2}}\] \[ \Large \boldsymbol{A = 127,31~cm^2}\]Für alle, die sich gerne selbst kontrollieren möchten, ob sie richtig gerechnet haben, habe ich hier etwas eingefügt. Gebt bitte die Anzahl der Ecken in das
obere schattierte Feld ein und darunter in das Feld die Seitenlänge des regelmäßigen n-Ecks. Schon kommt das Ergebnis im grünen Feld (wenn hoffentlich Javascrpt aktiviert ist...).
Noch ein n-eck rechnen? Kein Problem. Einfach wieder in die Felder klicken, die alten Zahlen löschen und die neuen reinschreiben. Viel Spaß damit!