Gerade in der jetzigen heißt es immer wieder, dass wir Abstand halten sollen. Aber was ist Abstand in der Mathematik eigentlich? Wie bestimmen wir den Abstand? Diese Fragen werde ich in diesem Kapitel beantworten. Ich beschränke mich dabei auf die beiden wichtigsten mathematischen Abstände, nämlich den Abstand zweier Punkte und den Abstand eines Punktes von einer Geraden (oder auch einer geraden Linie).
Wenn man in der Mathematik vom Abstand spricht, meint manimmer denkürzesten Weg zwischen zwei Objekten.
Nehmen wir uns zunächst den Abstand zwischen zwei Punkten vor.

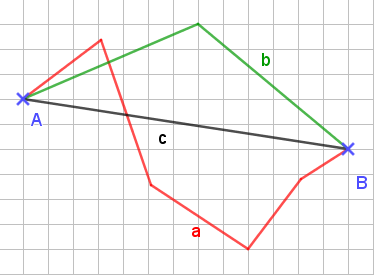
Wir sehen die beiden Punkte A und B. Es sind drei Wege eingezeichnet, um von A nach B zu kommen. Alle sind unterschiedlich lang und nur der Weg c ist der kürzeste. Der liegt auf einer geraden Linie. Das kann man allgemein formulieren:
Für die Praxis:
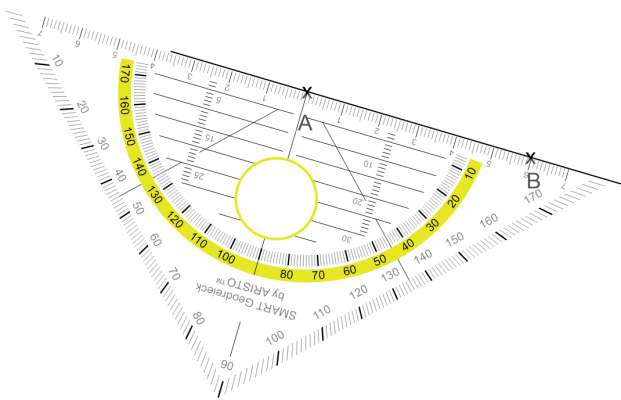
Wir zeichnen eine Gerade durch die beiden Punkte und messen dann die Strecke zwischen A und B. Wenn wir also einen Abstand von 1,50 m von einer zweiten Person halten sollen, muss das in gerader Linie gemessen sein.
Wie sieht das jetzt aber aus, wenn ich einen Punkt und eine Gerade habe?
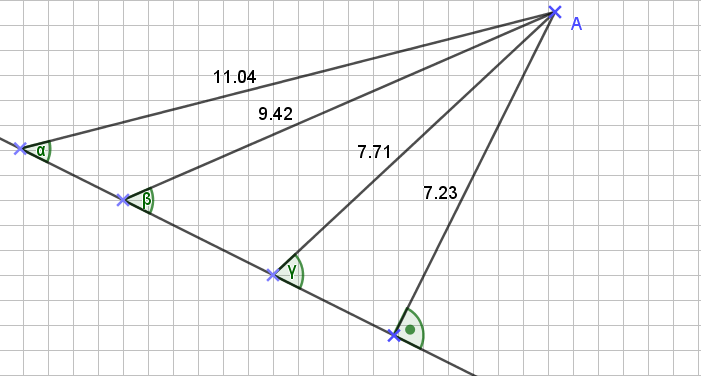
Auch hier müsste der Abstand auf einer Gerade liegen. Doch welcher der eingezeichneten Strecken ist nun der richtige?
Wir sehen, dass die Länge der Strecke zwischen A und der Geraden immer kleiner wird, je mehr sich der Winkel 90° annähert. Diejenige Strecke, die mit der Geraden einen rechten Winkel bildet, muss offenbar die kürzeste sein und damit unsere gesuchte Lösung.
Auch hier zeige ich euch zwei Verfahren, wie man das lösen kann. Das erste ist im strengen Sinn kein mathematisches Verfahren und in dieser Form erst seit 1964 möglich. Seitdem gibt es nämlich das Geodreieck in der auch heute noch gebräuchlichen Form (Das heißt, ich musste am Anfang meines Schullebens ohne Geodreieck auskommen… Ich habe es erst in der 7. Klasse bekommen.). Das zweite ist ein zeichnerisches Verfahren und mit der hehren Mathematik vereinbar 😉
Kommen wir zum Geodreieck:
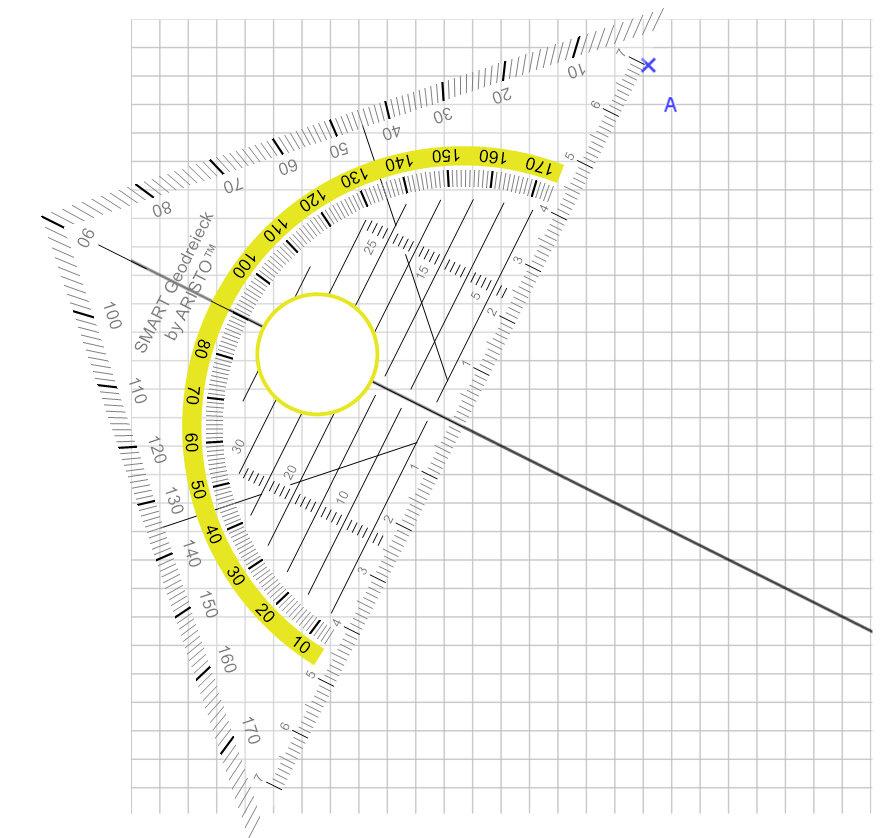
Wir legen das Geodreieck mit der Mittellinie auf die Gerade. Wir wissen, dass die Mittellinie des Geodreiecks mit der Basis einen rechten Winkel bildet. Wir verschieben das Geodreieck nun solange, bis die lange Seite den Punkt A trifft. Dann lesen wir einfach ab. Hier sind es 7 cm. Fertig...
Und nun kommen wir zum zeichnerischen Verfahren. Das wird tatsächlich noch weitgehend genutzt, weil z.B. die angelsächsischen Länder das Geodreieck kaum kennen und nutzen.
Wir sehen wieder den Punkt A und die Gerade.
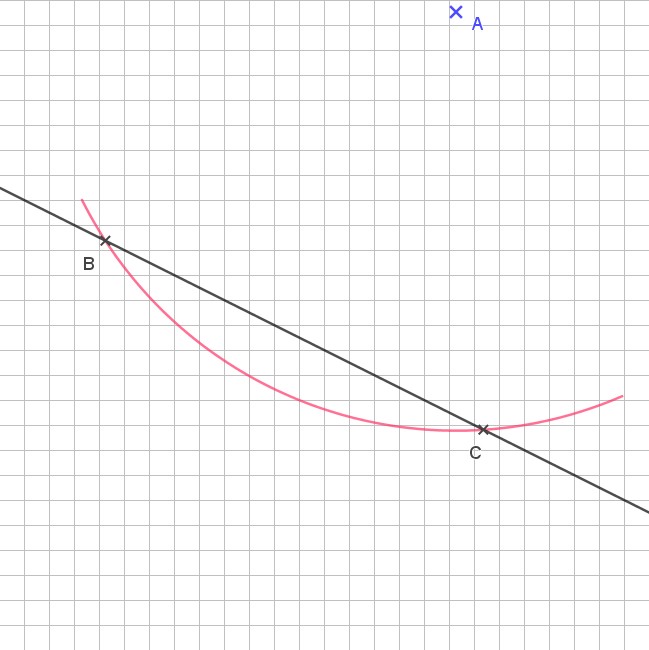
Wir nehmen einen Zirkel, stechen in A ein und ziehen einen Kreisbogen (rote Linie). Der Radius muss so groß sein, dass die Gerade in zwei Punkten B und C geschnitten wird.
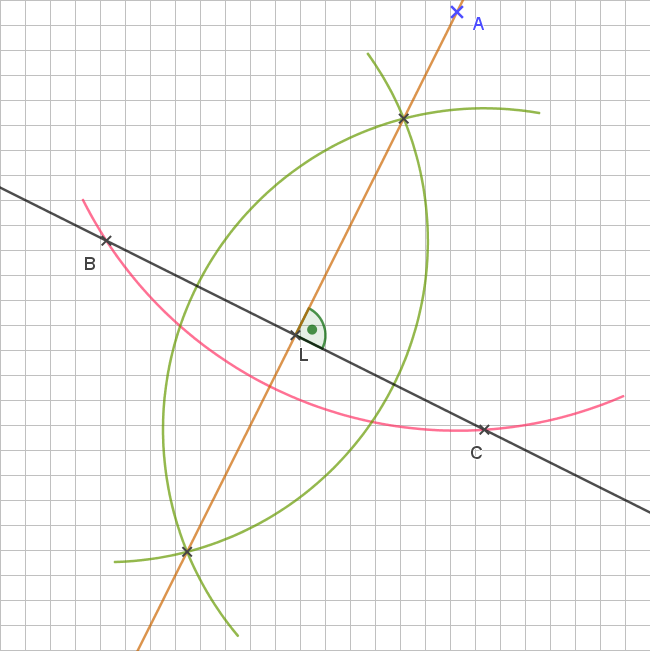
Nun zeichnen wir um B und um C jeweils einen Kreisbogen (grüne Linien) mit einem jeweils gleich großen Radius. Der Radius muss so groß sein, dass die beiden Kreisbögen sich schneiden.
Durch diese beiden Schnittpunkte zeichnen wir eine Gerade (braune Linie). Diese schneidet die Ausgangsgerade in L, steht senkrecht zu ihr und geht durch A. Die Strecke zwischen L und A können wir dann messen.
Für Spezialisten:
Das ist das Verfahren des Lotfällens. Das Lot von einem Punkt auf eine Gerade steht immer senkrecht auf der Geraden. Wir haben hier das Lot von A auf die Gerade gefällt. Den Punkt L nennen wir Lotpunkt zu A. Damit steht die Strecke zwischen L und A senkrecht auf der Geraden und ist der gesuchte Abstand.